
¿Has tocado alguna vez un cilindro neumático después de un funcionamiento continuo y se ha sorprendido de lo caliente que se siente? Ese calor no es sólo un inconveniente: representa un derroche de energía, una reducción de la eficiencia y posibles problemas de fiabilidad que podrían costarle miles de euros a su empresa.
La transferencia de calor en los sistemas neumáticos se produce a través de tres mecanismos: conducción a través de los materiales de los componentes, convección entre las superficies y el aire, y radiación desde las superficies calientes. Comprender y optimizar estos principios puede reducir las temperaturas de funcionamiento entre 15 y 30%, prolongar la vida útil de los componentes hasta 40% y mejorar la eficiencia energética entre 5 y 15%.
El mes pasado, trabajé como consultor para una planta de procesamiento de alimentos de Georgia en la que sus cilindros sin vástago fallaban cada 3-4 meses debido a problemas térmicos. Su equipo de mantenimiento se limitaba a sustituir componentes sin abordar la causa principal. Aplicando principios adecuados de transferencia de calor, redujimos las temperaturas de funcionamiento en 22 °C y alargamos la vida útil de los componentes a más de un año. Permítame mostrarle cómo lo hicimos y cómo puede aplicar estos mismos principios a sus sistemas.
Índice
- Cálculo del coeficiente de conducción: ¿Cómo se desplaza el calor a través de sus componentes?
- Métodos de mejora de la convección: ¿Qué técnicas maximizan la transferencia de calor aire-superficie?
- Modelo de eficiencia de la radiación: ¿Cuándo es importante la radiación térmica en los sistemas neumáticos?
- Conclusión
- Preguntas frecuentes sobre la transferencia de calor en sistemas neumáticos
Cálculo del coeficiente de conducción: ¿Cómo se desplaza el calor a través de sus componentes?
La conducción es el principal mecanismo de transferencia de calor dentro de los componentes neumáticos sólidos. Saber calcular y optimizar los coeficientes de conducción es esencial para gestionar las temperaturas del sistema.
El coeficiente de conducción del calor puede calcularse mediante Ley de Fourier1q = -k(dT/dx), donde q es el flujo de calor (W/m²), k es la conductividad térmica (W/m-K) y dT/dx es el gradiente de temperatura. En el caso de los componentes neumáticos, la conducción efectiva depende de la selección del material, la calidad de la interfaz y los factores geométricos que afectan a la longitud de la trayectoria térmica y el área de la sección transversal.
Recuerdo haber solucionado problemas en una línea de fabricación de Tennessee en la que los cojinetes de los cilindros sin vástago fallaban prematuramente. El equipo de mantenimiento había probado varios lubricantes sin éxito. Cuando analizamos las vías de conducción, descubrimos un cuello de botella térmico en la interfaz entre el rodamiento y la carcasa. Al mejorar el acabado de la superficie y aplicar un compuesto conductor térmico, aumentamos el coeficiente de conducción efectivo en 340% y eliminamos los fallos por completo.
Ecuaciones fundamentales de conducción
Desglosemos las ecuaciones clave para calcular la conducción en los componentes neumáticos:
Ley de Fourier para la conducción del calor
La ecuación básica que rige la conducción del calor es:
q = -k(dT/dx)
Dónde:
- q = Flujo de calor (W/m²)
- k = Conductividad térmica (W/m-K)
- dT/dx = Gradiente de temperatura (K/m)
Para un caso unidimensional simple con sección transversal constante:
Q = kA(T₁-T₂)/L
Dónde:
- Q = tasa de transferencia de calor (W)
- A = Superficie de la sección transversal (m²)
- T₁, T₂ = Temperaturas en cada extremo (K).
- L = Longitud del recorrido térmico (m)
Concepto de resistencia térmica
Para geometrías complejas, el enfoque de la resistencia térmica suele ser más práctico:
R = L/(kA)
Dónde:
- R = Resistencia térmica (K/W)
Para sistemas con varios componentes en serie:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
Y la tasa de transferencia de calor se convierte en:
Q = ΔT/Rtotal
Comparación de la conductividad térmica de los materiales
| Material | Conductividad térmica (W/m-K) | Conductividad relativa | Aplicaciones comunes |
|---|---|---|---|
| Aluminio | 205-250 | Alta | Cilindros, disipadores de calor |
| Acero | 36-54 | Medio | Componentes estructurales |
| Acero inoxidable | 14-16 | Bajo-Medio | Entornos corrosivos |
| Bronce | 26-50 | Medio | Cojinetes, casquillos |
| PTFE | 0.25 | Muy bajo | Juntas, rodamientos |
| Caucho nitrílico | 0.13 | Muy bajo | Juntas tóricas |
| Aire (sin gas) | 0.026 | Extremadamente bajo | Relleno de huecos |
| Pasta térmica | 3-8 | Bajo | Material de interfaz |
Resistencia de contacto en conjuntos neumáticos
En las interfaces entre componentes, la resistencia de contacto afecta significativamente a la transferencia de calor:
Rcontacto = 1/(hc × A)
Dónde:
- hc = Coeficiente de contacto (W/m²-K)
- A = Superficie de contacto (m²)
Entre los factores que afectan a la resistencia de contacto se incluyen:
- Rugosidad superficial: Las superficies más rugosas tienen menos superficie de contacto real
- Contacto Presión: Una mayor presión aumenta la superficie de contacto efectiva
- Materiales de interfaz: Los compuestos térmicos rellenan los huecos de aire
- Limpieza de superficies: Los contaminantes pueden aumentar la resistencia
Caso práctico: Optimización térmica de cilindros sin vástago
Para un cilindro magnético sin vástago con problemas térmicos:
| Componente | Diseño original | Diseño optimizado | Mejora |
|---|---|---|---|
| Cuerpo del cilindro | Aluminio anodizado | Mismo material, mejor acabado | 15% mejor conducción |
| Interfaz de rodamientos | Contacto metal con metal | Compuesto térmico añadido | 340% mejor conducción |
| Soportes de montaje | Acero pintado | Aluminio desnudo | 280% mejor conducción |
| Resistencia térmica global | 2,8 K/W | 0,7 K/W | Reducción 75% |
| Temperatura de funcionamiento | 78°C | 56°C | Reducción de 22°C |
| Vida útil de los componentes | 4 meses | >12 meses | 3× mejora |
Técnicas prácticas de optimización de la conducción
Basándome en mi experiencia con cientos de sistemas neumáticos, he aquí los enfoques más eficaces para mejorar la conducción:
Optimización de interfaces
- Acabado de superficies: Mejora la suavidad de la superficie de contacto hasta Ra 0,4-0,8 μm.
- Materiales de interfaz térmica2: Aplicar compuestos adecuados (3-8 W/m-K)
- Par de apriete: Asegurar un apriete correcto para una presión de contacto óptima
- Limpieza: Elimine todos los aceites y contaminantes antes del montaje
Estrategias de selección de materiales
- Vías críticas de calor: Utilizar materiales de alta conductividad (aluminio, cobre)
- Roturas térmicas: Utilizar intencionadamente materiales de baja conductividad para aislar el calor.
- Enfoques compuestos: Combinación de materiales para un rendimiento/coste óptimos
- Materiales anisótropos: Utilizar la conductividad direccional cuando proceda
Optimización geométrica
- Longitud de la trayectoria térmica: Minimizar la distancia entre fuentes de calor y disipadores
- Sección transversal: Maximizar el área perpendicular al flujo de calor
- Cuellos de botella térmicos: Identificar y eliminar las constricciones en la trayectoria del calor
- Vías redundantes: Crear múltiples vías de conducción paralelas
Métodos de mejora de la convección: ¿Qué técnicas maximizan la transferencia de calor aire-superficie?
La convección suele ser el factor limitante en la refrigeración de sistemas neumáticos. Potenciar la transferencia de calor por convección puede mejorar drásticamente la gestión térmica y el rendimiento del sistema.
La transferencia de calor por convección es la siguiente Ley de enfriamiento de Newton3: Q = hA(Ts-T∞), donde h es el coeficiente de convección (W/m²-K), A es el área superficial y (Ts-T∞) es la diferencia de temperatura entre la superficie y el fluido. Los métodos de mejora incluyen el aumento de la superficie mediante aletas, la mejora de la velocidad del fluido con un flujo de aire dirigido y la optimización de las características de la superficie para favorecer las capas límite turbulentas.
Durante una auditoría de eficiencia energética en unas instalaciones de envasado de Arizona, me encontré con un sistema neumático que funcionaba en un entorno con una temperatura ambiente de 43 °C. Sus cilindros sin vástago se sobrecalentaban a pesar de cumplir todos los requisitos de mantenimiento. Mediante la aplicación de una mejora de la convección específica -añadiendo pequeñas aletas de aluminio y un ventilador de bajo consumo- aumentamos el coeficiente de convección en 450%. Esto redujo las temperaturas de funcionamiento de niveles peligrosos a valores dentro de las especificaciones sin necesidad de realizar modificaciones importantes en el sistema.
Fundamentos de la transferencia de calor por convección
La ecuación básica que rige la transferencia de calor por convección es:
Q = hA(Ts-T∞)
Dónde:
- Q = tasa de transferencia de calor (W)
- h = Coeficiente de convección (W/m²-K)
- A = Superficie (m²)
- Ts = Temperatura de la superficie (K)
- T∞ = Temperatura del fluido (aire) (K)
El coeficiente de convección h depende de múltiples factores:
- Propiedades de los fluidos (densidad, viscosidad, conductividad térmica)
- Características del flujo (velocidad, turbulencia)
- Geometría y orientación de la superficie
- Régimen de flujo (convección natural frente a convección forzada)
Convección natural frente a forzada
| Parámetro | Convección natural | Convección forzada | Implicaciones |
|---|---|---|---|
| Valor h típico | 5-25 W/m²-K | 25-250 W/m²-K | La convección forzada puede ser 10 veces más eficaz |
| Fuerza motriz | Flotabilidad (diferencia de temperatura) | Presión externa (ventiladores, sopladores) | La convección forzada depende menos de la temperatura |
| Patrón de flujo | Flujo vertical a lo largo de superficies | Direccional basado en el mecanismo de forzamiento | El flujo forzado puede optimizarse para componentes específicos |
| Fiabilidad | Pasivo, siempre presente | Requiere energía y mantenimiento | La convección natural proporciona una refrigeración básica |
| Espacio necesario | Requiere espacio libre para la circulación del aire | Requiere espacio para ventiladores y conductos | Los sistemas forzados necesitan más planificación |
Técnicas de mejora de la convección
Aumento de la superficie
Aumento de la superficie efectiva mediante:
Aletas y superficies extendidas
- Aletas de pin: Flujo de aire omnidireccional, aumento de área 150-300%
- Aletas de placa: Flujo de aire direccional, aumento de área 200-500%
- Superficies onduladas: Mejora moderada, aumento de superficie 50-150%Desbaste de superficies
- Microtexturizado: 5-15% aumento efectivo de la superficie
- Superficies con hoyuelos: aumento de 10-30% más efectos de capa límite
- Patrones ranurados: 15-40% aumento con beneficios direccionales
Manipulación de flujos
Mejora de las características del flujo de aire mediante:
Sistemas de aire forzado
- Ventiladores: flujo de aire direccional, 200-600% h mejora
- Soplantes: Flujo de alta presión, 300-800% h mejora
- Chorros de aire comprimido: Enfriamiento dirigido, 400-1000% mejora local hOptimización de la trayectoria del flujo
- Deflectores: Aire directo a los componentes críticos
- Efectos Venturi: Aceleran el aire sobre superficies específicas
- Generadores de vórtices: Crean turbulencias para alterar la capa límite
Modificaciones de superficie
Alteración de las propiedades de la superficie para mejorar la convección:
Tratamientos de emisividad
- Óxido negro: Aumenta la emisividad a 0,7-0,9
- Anodizado: Emisividad controlada de 0,4-0,9
- Pinturas y revestimientos: Emisividad personalizable hasta 0,98Control de la humectabilidad
- Recubrimientos hidrófilos: Mejoran la refrigeración líquida
- Superficies hidrófobas: Evitan los problemas de condensación
- Mojabilidad estampada: Flujo de condensado dirigido
Ejemplo práctico de aplicación
Para un cilindro neumático sin vástago que funciona en un entorno de alta temperatura:
| Método de mejora | Aplicación | h Mejora | Reducción de la temperatura |
|---|---|---|---|
| Aletas de pasador (6 mm) | Aletas de aluminio con clip, separación de 10 mm | 180% | 12°C |
| Flujo de aire dirigido | Ventilador de corriente continua de 80 mm y 2 W a 1,5 m/s | 320% | 18°C |
| Tratamiento de superficies | Anodizado negro | 40% | 3°C |
| Enfoque combinado | Todos los métodos integrados | 450% | 24°C |
Correlación del número Nusselt para cálculos de diseño
Para los cálculos de ingeniería, el Número Nusselt4 (Nu) proporciona una aproximación adimensional a la convección:
Nu = hL/k
Dónde:
- L = Longitud característica
- k = Conductividad térmica del fluido
Para la convección forzada sobre una placa plana:
Nu = 0,664Re^(1/2)Pr^(1/3) (flujo laminar)
Nu = 0,037Re^(4/5)Pr^(1/3) (flujo turbulento)
Dónde:
- Re = número de Reynolds (velocidad × longitud × densidad / viscosidad)
- Pr = número de Prandtl (calor específico × viscosidad / conductividad térmica)
Estas correlaciones permiten a los ingenieros predecir los coeficientes de convección para distintas configuraciones y optimizar en consecuencia las estrategias de refrigeración.
Modelo de eficiencia de la radiación: ¿Cuándo es importante la radiación térmica en los sistemas neumáticos?
La radiación suele pasarse por alto en la gestión térmica de los sistemas neumáticos, pero puede representar el 15-30% de la transferencia total de calor en muchas aplicaciones. Entender cuándo y cómo optimizar la transferencia de calor radiativo es crucial para una gestión térmica integral.
La transferencia de calor por radiación sigue la Ley de Stefan-Boltzmann5: Q = εσA(T₁⁴-T₂⁴), donde ε es la emisividad de la superficie, σ es la constante de Stefan-Boltzmann, A es el área de la superficie, y T₁ y T₂ son las temperaturas absolutas de la superficie emisora y del entorno. La eficiencia de la radiación en los sistemas neumáticos depende principalmente de la emisividad de la superficie, el diferencial de temperatura y los factores de visión entre los componentes y su entorno.
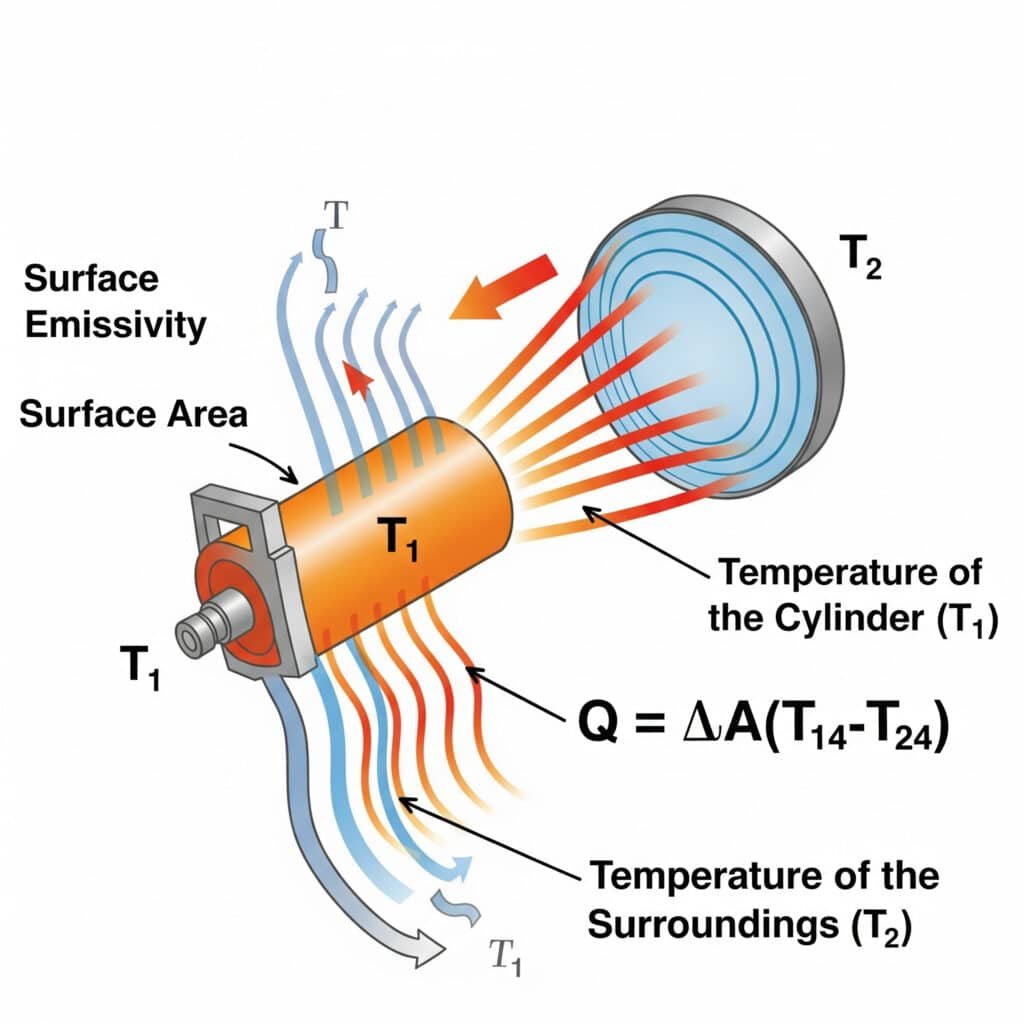
Hace poco ayudé a un fabricante de equipos semiconductores de Oregón a resolver los problemas de sobrecalentamiento de sus cilindros de precisión sin vástago. Sus ingenieros se habían centrado exclusivamente en la conducción y la convección, pero habían pasado por alto la radiación. Aplicando un revestimiento de alta emisividad (aumentando ε de 0,11 a 0,92), mejoramos la transferencia de calor por radiación en más de 700%. Esta solución sencilla y pasiva redujo la temperatura de funcionamiento en 9 °C sin piezas móviles ni consumo de energía, un requisito esencial en el entorno de la sala blanca.
Fundamentos de la transferencia de calor por radiación
La ecuación básica que rige la transferencia de calor por radiación es:
Q = εσA(T₁⁴-T₂⁴)
Dónde:
- Q = tasa de transferencia de calor (W)
- ε = Emisividad (adimensional, 0-1)
- σ = constante de Stefan-Boltzmann (5,67 × 10-⁸ W/m²-K⁴)
- A = Superficie (m²)
- T₁ = Temperatura absoluta de la superficie (K)
- T₂ = Temperatura absoluta del entorno (K)
Valores de emisividad superficial de los materiales neumáticos más comunes
| Material/Superficie | Emisividad (ε) | Eficacia de la radiación | Potencial de mejora |
|---|---|---|---|
| Aluminio pulido | 0.04-0.06 | Muy deficiente | >1500% mejora posible |
| Aluminio anodizado | 0.7-0.9 | Excelente | Ya optimizado |
| Acero inoxidable (pulido) | 0.07-0.14 | Pobre | >600% mejora posible |
| Acero inoxidable (oxidado) | 0.6-0.85 | Bien | Posible mejora moderada |
| Acero (pulido) | 0.07-0.10 | Pobre | >900% mejora posible |
| Acero (oxidado) | 0.7-0.9 | Excelente | Ya optimizado |
| Superficies pintadas | 0.8-0.98 | Excelente | Ya optimizado |
| PTFE (blanco) | 0.8-0.9 | Excelente | Ya optimizado |
| Caucho nitrílico | 0.86-0.94 | Excelente | Ya optimizado |
Ver Factor Consideraciones
El intercambio de radiación no sólo depende de la emisividad, sino también de las relaciones geométricas entre las superficies:
F₁₂ = Fracción de radiación que sale de la superficie 1 e incide en la superficie 2.
Para geometrías complejas, los factores de vista pueden calcularse utilizando:
- Soluciones analíticas para geometrías simples
- Ver álgebra factorial para combinar soluciones conocidas
- Métodos numéricos para disposiciones complejas
- Aproximaciones empíricas para la ingeniería práctica
Dependencia de la temperatura de la radiación
La relación de temperatura de cuarta potencia hace que la radiación sea especialmente eficaz a temperaturas más elevadas:
| Temperatura de la superficie | Porcentaje de transferencia de calor por radiación*. |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Suponiendo condiciones de convección natural, ε = 0,8, 25°C ambiente.
Estrategias de mejora de la eficiencia de la radiación
Basándome en mi experiencia con sistemas neumáticos industriales, he aquí los enfoques más eficaces para mejorar la transferencia de calor por radiación:
Modificación de la emisividad de la superficie
Revestimientos de alta emisividad
- Anodizado negro para aluminio (ε ≈ 0,8-0,9)
- Óxido negro para acero (ε ≈ 0,7-0,8)
- Recubrimientos cerámicos especiales (ε ≈ 0,9-0,98)Texturizado de superficies
- El microrrugoso aumenta la emisividad efectiva
- Las superficies porosas mejoran las propiedades radiativas
- Mejoras combinadas de emisividad/convección
Optimización medioambiental
Gestión de la temperatura ambiente
- Blindaje de equipos/procesos calientes
- Paredes y techos fríos para mejorar el intercambio de radiación
- Barreras reflectantes para dirigir la radiación a superficies más fríasVer factor de mejora
- Orientación para maximizar la exposición a superficies frías
- Eliminación de objetos que bloquean
- Reflectores para mejorar el intercambio de radiación con zonas más frías
Estudio de caso: Mejora de la radiación en la neumática de precisión
Para un cilindro sin vástago de alta precisión en un entorno de sala limpia:
| Parámetro | Diseño original | Diseño con radiación mejorada | Mejora |
|---|---|---|---|
| Superficie Material | Aluminio pulido (ε ≈ 0,06) | Aluminio con revestimiento cerámico (ε ≈ 0,94) | 1467% aumento de la emisividad |
| Transferencia de calor por radiación | 2.1W | 32.7W | 1457% aumento de la radiación |
| Temperatura de funcionamiento | 68°C | 59°C | Reducción de 9°C |
| Vida útil de los componentes | 8 meses | >24 meses | 3× mejora |
| Coste de aplicación | – | $175 por cilindro | 4,2 meses de amortización |
Radiación frente a otros modos de transferencia de calor
Comprender cuándo domina la radiación es crucial para una gestión térmica eficaz:
| Condición | Dominio de la conducción | Dominio de la convección | Dominio de la radiación |
|---|---|---|---|
| Temperatura | De bajo a alto | Bajo a medio | Media a alta |
| Propiedades de los materiales | Materiales de alto k | Bajo k, alta superficie | Superficies de ε alto |
| Factores medioambientales | Buen contacto térmico | Aire en movimiento, ventiladores | Gran diferencial de temperatura |
| Limitaciones de espacio | Embalaje hermético | Flujo de aire abierto | Vista a un entorno más fresco |
| Mejores aplicaciones | Interfaces de componentes | Refrigeración general | Superficies calientes, vacío, aire en calma |
Conclusión
El dominio de los principios de transferencia de calor (cálculo del coeficiente de conducción, métodos de mejora de la convección y modelado de la eficiencia de la radiación) sienta las bases para una gestión térmica eficaz de los sistemas neumáticos. La aplicación de estos principios permite reducir las temperaturas de funcionamiento, prolongar la vida útil de los componentes y mejorar la eficiencia energética, al tiempo que se garantiza un funcionamiento fiable incluso en entornos difíciles.
Preguntas frecuentes sobre la transferencia de calor en sistemas neumáticos
¿Cuál es el aumento típico de temperatura en los cilindros neumáticos durante su funcionamiento?
Los cilindros neumáticos suelen experimentar aumentos de temperatura de 20-40 °C por encima de la temperatura ambiente durante su funcionamiento continuo. Este aumento se debe a la fricción entre las juntas y las paredes del cilindro, al calentamiento del aire por compresión y a la conversión del trabajo mecánico en calor. Los cilindros sin vástago suelen experimentar aumentos de temperatura más elevados (30-50°C) debido a sus sistemas de estanquidad más complejos y a la generación de calor concentrado en el conjunto cojinete/junta.
¿Cómo afecta la presión de funcionamiento a la generación de calor en los sistemas neumáticos?
La presión de funcionamiento tiene un impacto significativo en la generación de calor, ya que las presiones más altas crean más calor a través de varios mecanismos. Cada aumento de 1 bar en la presión de funcionamiento suele aumentar la generación de calor en 8-12% debido a las mayores fuerzas de fricción entre las juntas y las superficies, el mayor calentamiento por compresión y el aumento de las pérdidas relacionadas con las fugas. Esta relación es aproximadamente lineal dentro de los rangos de funcionamiento normales (3-10 bar).
¿Cuál es el método de refrigeración óptimo para los componentes neumáticos en distintos entornos?
El método de refrigeración óptimo varía según el entorno: en entornos limpios y de temperatura moderada (15-30 °C), suele bastar con la convección natural con una separación adecuada de los componentes. En entornos de alta temperatura (30-50°C), se hace necesaria la convección forzada mediante ventiladores o aire comprimido. En condiciones de calor extremo (>50°C) o cuando el flujo de aire está restringido, pueden ser necesarios métodos de refrigeración activa como refrigeradores termoeléctricos o refrigeración líquida. En todos los casos, la maximización de la radiación a través de superficies de alta emisividad proporciona una refrigeración pasiva adicional.
¿Cómo se calcula la transferencia total de calor de un componente neumático?
Calcular la transferencia total de calor sumando las contribuciones de cada mecanismo: Qtotal = Qconducción + Qconvección + Qradiación. Para la conducción, utilice Q = kA(T₁-T₂)/L para cada vía de calor. Para la convección, utilice Q = hA(Ts-T∞) con los coeficientes de convección adecuados. Para la radiación, utilice Q = εσA(T₁⁴-T₂⁴). En la mayoría de las aplicaciones neumáticas industriales que funcionan a 30-80°C, la distribución aproximada es 20-40% conducción, 40-70% convección y 10-30% radiación.
¿Qué relación hay entre la temperatura y la vida útil de los componentes neumáticos?
La vida útil de los componentes disminuye exponencialmente con el aumento de la temperatura, siguiendo una relación de Arrhenius modificada. Como regla general, cada aumento de 10°C en la temperatura de funcionamiento reduce la vida útil de las juntas y los componentes en 40-50%. Esto significa que un componente que funcione a 70°C puede durar sólo un tercio que el mismo componente a 50°C. Esta relación es especialmente crítica para los componentes de polímero como juntas, cojinetes y empaquetaduras, que a menudo determinan el intervalo de mantenimiento de los sistemas neumáticos.
-
Proporciona una explicación básica de la Ley de Fourier, el principio fundamental que describe cómo se conduce el calor a través de los materiales sólidos en función de su conductividad térmica y gradiente de temperatura. ↩
-
Explica la función y los tipos de materiales de interfaz térmica (TIM), que se utilizan para rellenar huecos de aire microscópicos entre componentes para mejorar la conducción del calor y reducir la resistencia térmica. ↩
-
Detalla los principios de la Ley de Newton del enfriamiento, que rige cómo los objetos se enfrían transfiriendo calor al fluido circundante por convección, un factor clave en el diseño de sistemas de refrigeración. ↩
-
Ofrece una visión en profundidad del número de Nusselt, una magnitud adimensional crítica en dinámica de fluidos y transferencia de calor que representa la relación entre la transferencia de calor convectiva y la conductiva a través de una frontera. ↩
-
Describe la ley de Stefan-Boltzmann, el principio físico fundamental que cuantifica la energía total irradiada por un cuerpo negro, esencial para calcular la pérdida de calor de las superficies calientes. ↩


