Con frecuencia, los ingenieros calculan mal las áreas de los vástagos cuando diseñan sistemas de cilindros neumáticos, lo que provoca cálculos de fuerza incorrectos y fallos en el rendimiento del sistema.
El área de la varilla es el área de la sección transversal circular calculada como A = πr² o A = π(d/2)², donde 'r' es el radio de la varilla y 'd' es el diámetro de la varilla, crítico para los cálculos de fuerza y presión.
Ayer ayudé a Carlos, un ingeniero de diseño de México, cuyo sistema neumático falló porque olvidó restar el área del vástago del área del pistón en sus cálculos de fuerza del cilindro de doble efecto.
Índice
- ¿Qué es el área del vástago en los sistemas de cilindros neumáticos?
- ¿Cómo se calcula la sección transversal de una barra?
- ¿Por qué es importante el área de la varilla para calcular la fuerza?
- ¿Cómo afecta el área del vástago al rendimiento del cilindro?
¿Qué es el área del vástago en los sistemas de cilindros neumáticos?
El área del vástago representa el área de la sección transversal circular del vástago, esencial para calcular las áreas efectivas del vástago y las salidas de fuerza en cilindros neumáticos de doble efecto.
El área del vástago es el área circular ocupada por la sección transversal del vástago, medida perpendicularmente al eje del vástago, utilizada para determinar las áreas efectivas netas para los cálculos de fuerza.
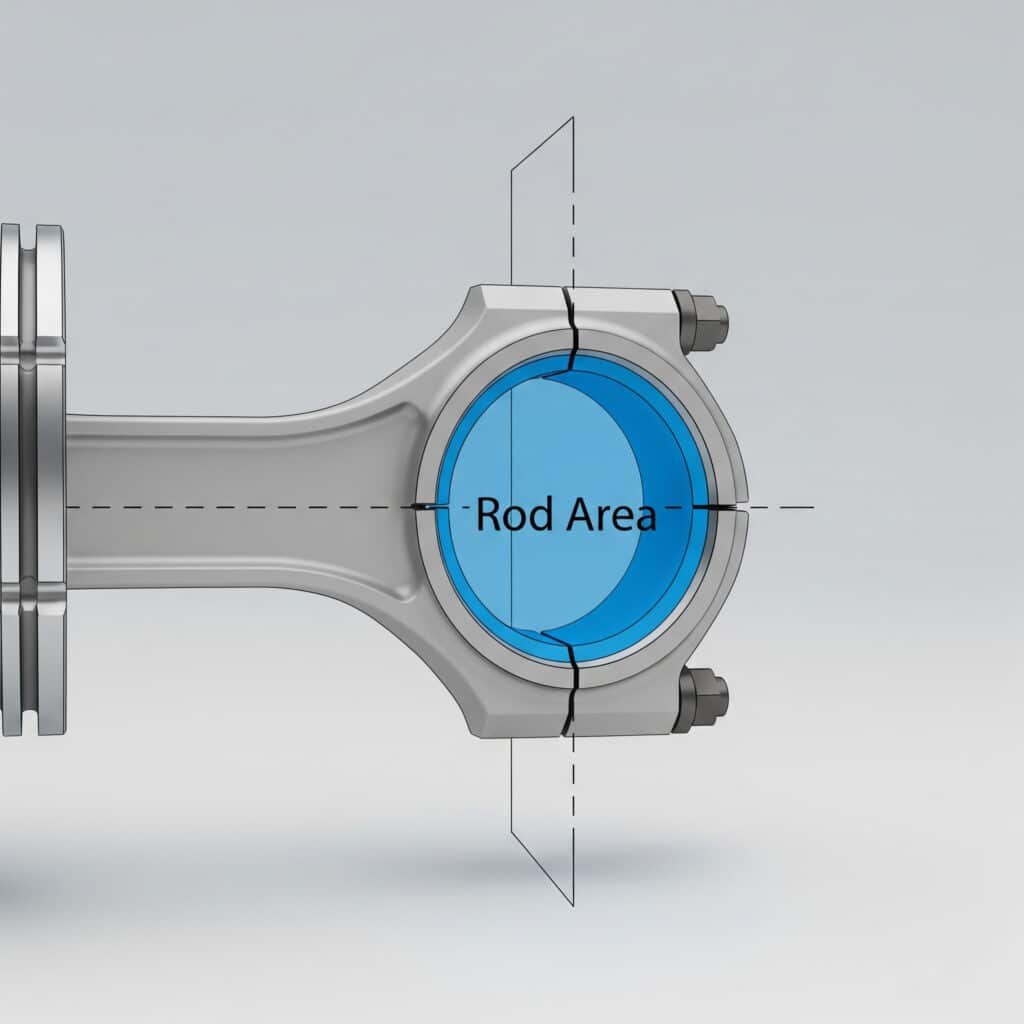
Definición del área de varillas
Propiedades geométricas
- Sección circular: Geometría de varilla estándar
- Medición perpendicular90° respecto a la línea central del vástago
- Superficie constante: Uniforme a lo largo de la varilla
- Área sólida: Sección transversal completa del material
Medidas clave
- Diámetro de la varilla: Dimensión principal para el cálculo de la superficie
- Radio de la varilla: Medida de la mitad del diámetro
- Sección transversal: Aplicación de la fórmula de área circular
- Área efectiva: Impacto en el rendimiento de los cilindros
Relación entre el área de la biela y el pistón
| Componente | Fórmula del área | Propósito | Aplicación |
|---|---|---|---|
| Pistón | A = π(D/2)² | Área de perforación completa | Ampliar el cálculo de fuerzas |
| Varilla | A = π(d/2)² | Sección transversal de la varilla | Cálculo de la fuerza de retracción |
| Superficie neta | A_pistón - A_varilla | Área de retracción efectiva | Cilindros de doble efecto |
| Área anular1 | π(D² - d²)/4 | Zona en forma de anillo | Presión lado varilla |
Tamaños de varilla estándar
Diámetros comunes de varilla
- Varilla de 8 mm: Superficie = 50,3 mm²
- Varilla de 12 mm: Superficie = 113,1 mm²
- Varilla de 16 mm: Superficie = 201,1 mm²
- Varilla de 20 mm: Superficie = 314,2 mm²
- Varilla de 25 mm: Superficie = 490,9 mm²
- Varilla de 32 mm: Superficie = 804,2 mm²
Relación varilla/taladro
- Relación estándar: Diámetro del vástago = 0,5 × diámetro del orificio
- Trabajo pesado: Diámetro del vástago = 0,6 × diámetro del orificio
- Trabajo ligero: Diámetro del vástago = 0,4 × diámetro del agujero
- Aplicaciones personalizadas: Según las necesidades
Aplicaciones del área de varillas
Cálculo de fuerzas
Utilizo el área de varillas para:
- Extender la fuerza: Área total del pistón × presión
- Fuerza de retracción(área del pistón - área del vástago) × presión
- Diferencial de fuerza: Diferencia entre extender/retraer
- Análisis de la carga: Adaptación del cilindro a la aplicación
Diseño del sistema
El área de la varilla afecta:
- Selección de cilindros: Dimensionamiento adecuado de las aplicaciones
- Cálculos de velocidad: Requisitos de caudal para cada sentido
- Requisitos de presión: Especificaciones de presión del sistema
- Optimización del rendimiento: Diseño de funcionamiento equilibrado
Superficie del vástago en diferentes tipos de cilindros
Cilindros de simple efecto
- Sin impacto en el área de la varilla: Retorno por muelle
- Sólo fuerza de extensión: Superficie total del pistón efectiva
- Cálculos simplificados: No se tiene en cuenta la fuerza de retracción
- Optimización de costes: Menor complejidad
Cilindros de doble efecto
- Área crítica de la varilla: Afecta a la fuerza de retracción
- Operación asimétrica: Fuerzas diferentes en cada dirección
- Cálculos complejos: Debe considerar ambas áreas
- Equilibrio de resultados: Consideraciones de diseño necesarias
Cilindros sin vástago
- Sin zona de varillas: Eliminado del diseño
- Operación simétrica: Fuerzas iguales en ambas direcciones
- Cálculos simplificados: Consideración de área única
- Ventajas espaciales: No es necesario prolongar la varilla
¿Cómo se calcula la sección transversal de una barra?
El cálculo del área de la sección transversal del vástago utiliza la fórmula estándar de área circular con medidas del diámetro o radio del vástago para un diseño preciso del sistema neumático.
Calcula el área de la varilla utilizando A = πr² (con radio) o A = π(d/2)² (con diámetro), donde π = 3,14159, asegurando unidades consistentes en todo el cálculo.
Fórmula básica del área
Uso del radio de la varilla
A = πr²
- A: Sección transversal de la varilla
- π: 3,14159 (constante matemática)
- r: Radio de la varilla (diámetro ÷ 2)
- Unidades: Área en unidades de radio al cuadrado
Utilización del diámetro de la varilla
A = π(d/2)² o A = πd²/4
- A: Sección transversal de la varilla
- π: 3.14159
- d: Diámetro de la varilla
- Unidades: Área en unidades de diámetro al cuadrado
Cálculo paso a paso
Proceso de medición
- Medir el diámetro de la varilla: Utilice calibradores para mayor precisión
- Verificar la medición: Realizar varias lecturas
- Calcular radior = diámetro ÷ 2 (si se utiliza la fórmula del radio)
- Aplicar fórmula: A = πr² o A = π(d/2)²
- Unidades de control: Garantizar la coherencia del sistema de unidades
Ejemplo de cálculo
Para una varilla de 20 mm de diámetro:
- Método 1: A = π(10)² = π × 100 = 314,16 mm².
- Método 2: A = π(20)²/4 = π × 400/4 = 314,16 mm².
- Verificación: Ambos métodos dan resultados idénticos
Tabla de cálculo del área de la varilla
| Diámetro de la varilla | Radio de la varilla | Cálculo de la superficie | Área de varillas |
|---|---|---|---|
| 8 mm | 4 mm | π × 4² | 50,3 mm² |
| 12 mm | 6 mm | π × 6² | 113,1 mm² |
| 16 mm | 8 mm | π × 8² | 201,1 mm² |
| 20 mm | 10 mm | π × 10² | 314,2 mm² |
| 25 mm | 12,5 mm | π × 12.5² | 490,9 mm² |
| 32 mm | 16 mm | π × 16² | 804,2 mm² |
Herramientas de medición
Calibres digitales
- PrecisiónPrecisión de ±0,02 mm
- Gama: 0-150mm típico
- Características: Pantalla digital, conversión de unidades
- Buenas prácticas: Múltiples puntos de medición
Micrómetro
- PrecisiónPrecisión de ±0,001 mm
- Gama: Varios tamaños disponibles
- Características: Tope de trinquete, opciones digitales
- Aplicaciones: Requisitos de alta precisión
Errores comunes de cálculo
Errores de medición
- Diámetro frente a radio: Utilización de una dimensión incorrecta en la fórmula
- Incoherencia de las unidades: Mezcla de mm y pulgadas
- Errores de precisión: Decimales insuficientes
- Calibrado de herramientas: Instrumentos de medida no calibrados
Errores de fórmula
- Fórmula incorrecta: Utilizar la circunferencia en lugar del área
- Falta π: Olvidar la constante matemática
- Errores de cuadratura: Aplicación incorrecta del exponente
- Conversión de unidades: Transformaciones unitarias inadecuadas
Métodos de verificación
Técnicas de comprobación cruzada
- Cálculos múltiples: Diferentes métodos de fórmula
- Verificación de medidas: Repetir las mediciones de diámetro
- Tablas de referencia: Comparación con valores estándar
- Software CAD: Cálculo del área del modelo 3D
Controles de razonabilidad
- Correlación de tamaño: Mayor diámetro = mayor superficie
- Comparaciones estándar: Coinciden con los tamaños típicos de las cañas
- Idoneidad de la aplicación: Adecuado al tamaño del cilindro
- Normas de fabricación: Tamaños comunes disponibles
Cálculos avanzados
Varillas huecas
A = π(D² - d²)/4
- D: Diámetro exterior
- d: Diámetro interior
- Aplicación: Reducción de peso, enrutamiento interno
- Cálculo: Resta el área interior del área exterior
Varillas no circulares
- Varillas cuadradas: A = lado²
- Varillas rectangulares: A = longitud × anchura
- Formas especiales: Utilizar fórmulas geométricas adecuadas
- Aplicaciones: Evitar la rotación, requisitos especiales
Cuando trabajé con Jennifer, una diseñadora de sistemas neumáticos de Canadá, inicialmente calculó el área del vástago de forma incorrecta al utilizar el diámetro en lugar del radio en la fórmula πr², lo que dio como resultado una sobreestimación de 4× y unos cálculos de fuerza completamente erróneos para su aplicación de cilindro de doble efecto.
¿Por qué es importante el área de la varilla para calcular la fuerza?
El área del vástago afecta directamente al área efectiva del pistón en el lado del vástago de los cilindros de doble efecto, creando diferencias de fuerza entre las operaciones de extensión y retracción.
El área del vástago reduce el área efectiva del pistón durante la retracción, creando una fuerza de retracción menor comparada con la fuerza de extensión en cilindros de doble efecto, lo que requiere una compensación en el diseño del sistema.
Fundamentos del cálculo de fuerzas
Fórmula básica de la fuerza
Fuerza = Presión × Superficie2
- Extender la fuerza: F = P × A_pistón
- Fuerza de retracción: F = P × (A_pistón - A_vástago)
- Diferencia de fuerza: Fuerza de extensión > Fuerza de retracción
- Impacto del diseño: Debe considerar ambas direcciones
Áreas efectivas
- Área completa del pistón: Disponible durante la prórroga
- Área neta del pistón: Superficie del pistón menos superficie del vástago durante la retracción
- Área anular: Zona en forma de anillo en el lado de la varilla
- Ratio de superficie: Determina el diferencial de fuerza
Ejemplos de cálculo de fuerzas
Cilindro de 63 mm de diámetro, vástago de 20 mm
- Área del pistón: π(31,5)² = 3.117 mm²
- Área de varillas: π(10)² = 314 mm²
- Superficie neta: 3.117 - 314 = 2.803 mm²
- A 6 bar de presión:
– Extender la fuerza: 6 × 3,117 = 18,702 N
– Fuerza de retracción: 6 × 2,803 = 16,818 N
– Diferencia de fuerza: 1.884 N (reducción 10%)
Tabla comparativa de fuerzas
| Tamaño del cilindro | Área del pistón | Área de varillas | Superficie neta | Relación de fuerzas |
|---|---|---|---|---|
| 32 mm/12 mm | 804 mm² | 113 mm² | 691 mm² | 86% |
| 50 mm/16 mm | 1.963 mm² | 201 mm | 1.762 mm² | 90% |
| 63 mm/20 mm | 3.117 mm² | 314 mm² | 2.803 mm² | 90% |
| 80 mm/25 mm | 5.027 mm² | 491 mm² | 4.536 mm² | 90% |
| 100 mm/32 mm | 7.854 mm² | 804 mm² | 7.050 mm² | 90% |
Impacto de la aplicación
Adaptación de la carga
- Ampliar cargas: Puede soportar toda la fuerza nominal
- Retraer cargas: Limitado por la reducción del área efectiva
- Equilibrio de la carga: Considerar el diferencial de fuerza en el diseño
- Márgenes de seguridad: Tener en cuenta la capacidad de repliegue reducida
Rendimiento del sistema
- Diferencias de velocidad: Diferentes requisitos de caudal en cada dirección
- Requisitos de presión: Puede necesitar mayor presión para retraerse
- Complejidad del control: Consideraciones sobre el funcionamiento asimétrico
- Eficiencia energética: Optimizar para ambas direcciones
Consideraciones sobre el diseño
Selección del tamaño de la varilla
- Ratios estándar: Diámetro del vástago = 0,5 × diámetro del orificio
- Cargas pesadas: Varilla más grande para mayor resistencia estructural
- Equilibrio de fuerzas: Varilla más pequeña para fuerzas más iguales
- Aplicación específica: Relaciones personalizadas para requisitos especiales
Estrategias de equilibrio de fuerzas
- Compensación de la presión: Mayor presión en el lado del vástago
- Compensación por superficie: Cilindro más grande para necesidades de retracción
- Cilindros dobles: Cilindros separados para cada dirección
- Diseño sin varillas: Elimina los efectos de área de las varillas
Aplicaciones prácticas
Manipulación de materiales
- Aplicaciones de elevación: Extender fuerza crítica
- Operaciones de empuje: Puede ser necesario ajustar la fuerza de retracción
- Sistemas de sujeción: El diferencial de fuerza afecta a la fuerza de retención
- Precisión de posicionamiento: Las variaciones de fuerza afectan a la precisión
Procesos de fabricación
- Operaciones de prensa: Requisitos de fuerza coherentes
- Sistemas de montaje: Se necesita un control preciso de la fuerza
- Control de calidad: Las variaciones de fuerza afectan a la calidad del producto
- Duración del ciclo: Diferencias de fuerza velocidad de impacto
Resolución de problemas de fuerza
Problemas comunes
- Fuerza de retracción insuficiente: Carga demasiado pesada para el área de la red
- Funcionamiento irregular: El diferencial de fuerzas causa problemas
- Variaciones de velocidad: Diferentes requisitos de caudal
- Dificultades de control: Características de respuesta asimétrica
Soluciones
- Aumento del tamaño de los cilindros: Mayor calibre para una fuerza de retracción adecuada
- Ajuste de la presión: Optimizar la dirección crítica
- Optimización del tamaño de la varilla: Equilibrar los requisitos de fuerza y resistencia
- Rediseño del sistema: Considere alternativas sin varilla
Cuando consulté con Michael, un constructor de máquinas de Australia, su equipo de envasado mostraba un funcionamiento incoherente porque lo había diseñado sólo para la fuerza de extensión. La reducción de la fuerza de retracción de la 15% provocaba atascos durante la carrera de retorno, por lo que era necesario aumentar el tamaño del cilindro para manejar correctamente ambas direcciones.
¿Cómo afecta el área del vástago al rendimiento del cilindro?
El área del vástago influye significativamente en la velocidad del cilindro, la fuerza de salida, el consumo de energía y el rendimiento general del sistema en aplicaciones neumáticas.
Las áreas de vástago más grandes reducen la fuerza de retracción y aumentan la velocidad de retracción debido a una menor área efectiva y menores requisitos de volumen de aire, lo que crea características de rendimiento asimétricas del cilindro.
Velocidad Rendimiento Impacto
Relaciones de caudal
Velocidad = Caudal3 ÷ Superficie efectiva
- Aumentar la velocidad: Caudal ÷ área total del pistón
- Velocidad de repliegue: Caudal ÷ (Superficie del pistón - Superficie del vástago)
- Diferencial de velocidad: Repliegue normalmente más rápido
- Optimización del flujo: Requisitos diferentes en cada dirección
Ejemplo de cálculo de la velocidad
Para diámetro interior de 63 mm, vástago de 20 mm y caudal de 100 L/min:
- Aumentar la velocidad: 100.000 ÷ 3.117 = 32,1 mm/s
- Velocidad de repliegue: 100.000 ÷ 2.803 = 35,7 mm/s
- Aumento de la velocidad: 11% retracción más rápida
Características de rendimiento
Efectos de salida de fuerza
| Tamaño de la varilla | Reducción de la fuerza | Aumento de velocidad | Impacto en el rendimiento |
|---|---|---|---|
| Pequeño (d/D = 0,3) | 9% | 10% | Asimetría mínima |
| Estándar (d/D = 0,5) | 25% | 33% | Asimetría moderada |
| Grande (d/D = 0,6) | 36% | 56% | Asimetría significativa |
Consumo de energía
- Extender la carrera: Se necesita todo el volumen de aire
- Carrera de retracción: Volumen de aire reducido (desplazamiento del vástago)
- Ahorro de energía: Menor consumo durante la retracción
- Eficacia del sistema: Posible optimización energética global
Análisis del consumo de aire
Cálculos de volumen
- Ampliar volumen: Superficie del pistón × longitud de la carrera
- Retraer volumen(Área del pistón - Área del vástago) × longitud de la carrera
- Diferencia de volumen: Ahorro de volumen de barras
- Impacto en los costes: Menor necesidad de compresores
Ejemplo de consumo
Diámetro de 100 mm, vástago de 32 mm, carrera de 500 mm:
- Ampliar volumen: 7.854 × 500 = 3.927.000 mm³
- Retraer volumen: 7.050 × 500 = 3.525.000 mm³
- Ahorro: 402.000 mm³ (reducción 10%)
Optimización del diseño del sistema
Criterios de selección del tamaño de la varilla
- Requisitos estructurales: Pandeo4 y cargas de flexión
- Equilibrio de fuerzas: Diferencial de fuerza aceptable
- Requisitos de velocidad: Características de velocidad deseadas
- Eficiencia energética: Optimización del consumo de aire
- Consideraciones económicas: Costes de material y fabricación
Equilibrio de resultados
- Control del caudal: Regulación separada para cada dirección
- Compensación de la presión: Ajustar a las necesidades de fuerza
- Adaptación de la velocidad: Acelerador dirección más rápida si es necesario
- Análisis de la carga: Adaptar el cilindro a las necesidades de la aplicación
Consideraciones específicas de la aplicación
Aplicaciones de alta velocidad
- Varillas pequeñas: Minimizar el diferencial de velocidad
- Optimización del flujo: Tamaño de las válvulas para cada dirección
- Complejidad del control: Gestionar la respuesta asimétrica
- Requisitos de precisión: Tener en cuenta las variaciones de velocidad
Aplicaciones pesadas
- Varillas grandes: Prioridad a la resistencia estructural
- Compensación de la fuerza: Aceptar fuerza de retracción reducida
- Análisis de la carga: Garantizar una capacidad adecuada en ambas direcciones
- Factores de seguridad: Enfoque de diseño conservador
Control del rendimiento
Indicadores clave de rendimiento
- Coherencia del tiempo de ciclo: Controlar las variaciones de velocidad
- Salida de fuerza: Verificar la capacidad adecuada
- Consumo de energía: Seguimiento de las pautas de uso del aire
- Presión del sistema: Optimizar la eficiencia
Pautas para la resolución de problemas
- Retracción lenta: Compruebe si hay un área de varilla excesiva
- Fuerza insuficiente: Verificar los cálculos del área efectiva
- Velocidades desiguales: Ajustar los controles de caudal
- Gran consumo de energía: Optimizar la selección del tamaño de la caña
Conceptos avanzados de rendimiento
Respuesta dinámica
- Diferencias de aceleración: Efectos de masa y área
- Características de resonancia: Variaciones de la frecuencia natural
- Control de la estabilidad: Comportamiento asimétrico del sistema
- Precisión de posicionamiento: Impactos del diferencial de velocidad
Efectos térmicos
- Generación de calor: Más alto en la dirección de extensión
- Aumento de la temperatura: Afecta a la coherencia del rendimiento
- Requisitos de refrigeración: Puede necesitar una disipación de calor mejorada
- Expansión del material: Consideraciones sobre el crecimiento térmico
Datos de rendimiento en el mundo real
Resultados del estudio de caso
El análisis de 100 instalaciones mostró:
- Relaciones de varilla estándar: 10-15% diferencial de velocidad típico
- Varillas sobredimensionadas: Hasta 50% de aumento de velocidad al replegarse
- Varillas subdimensionadas: Fallos estructurales en 25% de los casos.
- Diseños optimizados: Rendimiento equilibrado alcanzable
Cuando optimicé la selección de cilindros para Lisa, una ingeniera de embalajes del Reino Unido, redujimos el tamaño de su vástago de 0,6 a 0,5 de relación de diámetro interior, mejorando el equilibrio de fuerzas en 20% y manteniendo al mismo tiempo una resistencia estructural adecuada y reduciendo las variaciones del tiempo de ciclo en 30%.
Conclusión
El área del vástago es igual a π(d/2)² utilizando el diámetro "d" del vástago. Esta área reduce la fuerza de retracción efectiva en cilindros de doble efecto, creando diferencias de velocidad y fuerza que requieren consideración en el diseño del sistema neumático.
Preguntas frecuentes sobre el área de varillas
¿Cómo se calcula el área de las varillas?
Calcula el área de la varilla utilizando A = π(d/2)² donde "d" es el diámetro de la varilla, o A = πr² donde "r" es el radio de la varilla. Para una varilla de 20 mm de diámetro A = π(10)² = 314,2 mm².
¿Por qué es importante el área del vástago en los cilindros neumáticos?
El área del vástago reduce el área efectiva del pistón durante la retracción en cilindros de doble efecto, creando una fuerza de retracción menor en comparación con la fuerza de extensión. Esto afecta a los cálculos de fuerza, las características de velocidad y el rendimiento del sistema.
¿Cómo afecta el área del vástago a la fuerza del cilindro?
El área de la biela reduce la fuerza de retracción en la cantidad: Fuerza de retracción = Presión × (área del pistón - área del vástago). Un vástago de 20 mm en un cilindro de 63 mm reduce la fuerza de retracción en aproximadamente 10% en comparación con la fuerza de extensión.
¿Qué ocurre si se ignora el área de la varilla en los cálculos?
Ignorar el área del vástago conduce a cálculos de fuerza de retracción sobreestimados, cilindros subdimensionados para cargas de retracción, predicciones de velocidad incorrectas y fallos potenciales del sistema cuando el rendimiento real no coincide con las expectativas de diseño.
¿Cómo afecta el tamaño del vástago al rendimiento del cilindro?
Las varillas más grandes reducen más la fuerza de retracción pero aumentan la velocidad de retracción debido a la menor área efectiva. Las relaciones de varilla estándar (d/D = 0,5) proporcionan un buen equilibrio entre la resistencia estructural y la simetría de la fuerza en la mayoría de las aplicaciones.
-
Comprender la definición y el cálculo del área anular en contextos de ingeniería. ↩
-
Explore el principio físico fundamental, la Ley de Pascal, que rige los sistemas de potencia de fluidos. ↩
-
Descubra los principios del pandeo estructural, un modo de fallo crítico para los componentes esbeltos sometidos a compresión. ↩
-
Repasar la definición de caudal y su papel en el cálculo de la velocidad en los sistemas de fluidos. ↩



