¿Tiene problemas constantemente con los cálculos de sistemas neumáticos? Muchos ingenieros se enfrentan al mismo problema al diseñar o solucionar problemas de sistemas neumáticos. La buena noticia es que el dominio de unas pocas ecuaciones clave puede resolver la mayoría de sus retos neumáticos.
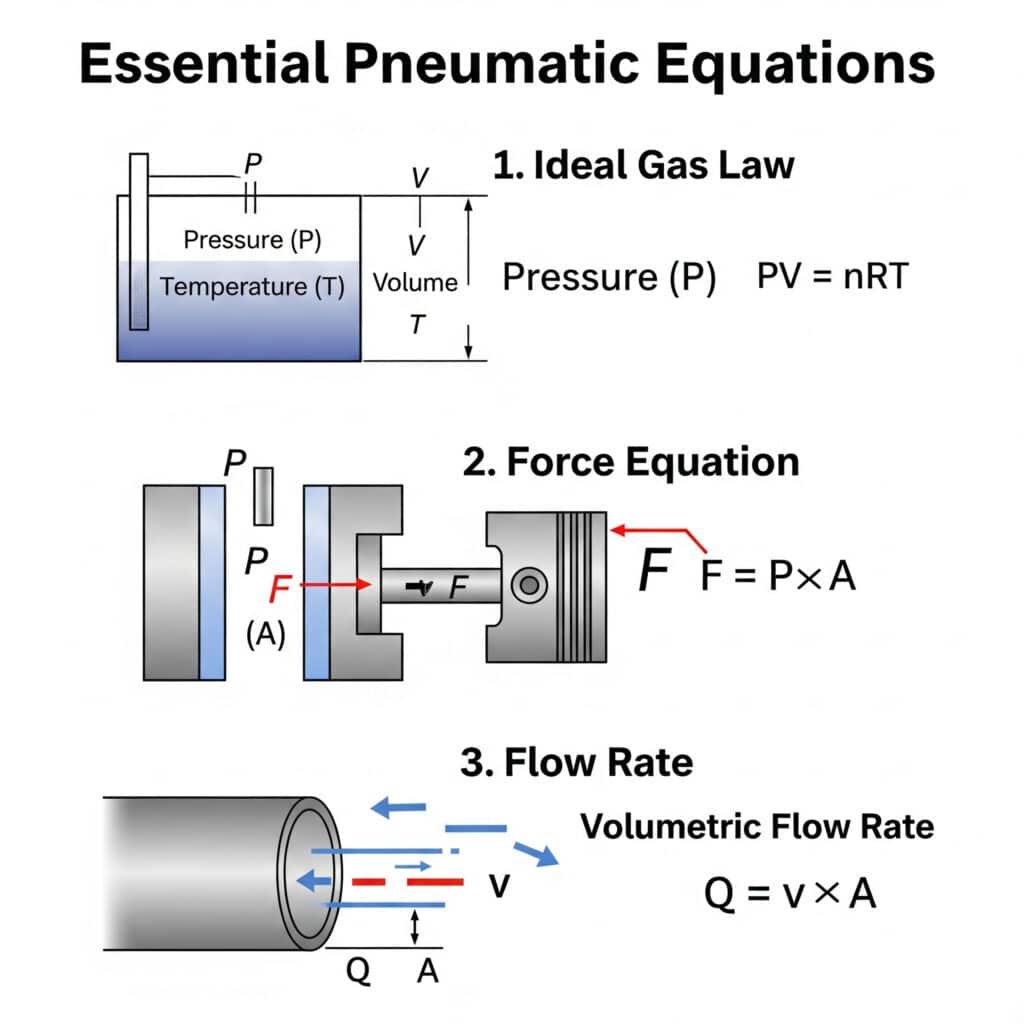
Las ecuaciones esenciales de la transmisión neumática que todo ingeniero debe conocer son las siguientes ley de los gases ideales (PV = nRT)1(F = P × A) y la relación de caudal (Q = v × A). Comprender estos fundamentos permite diseñar sistemas y solucionar problemas con precisión.
Llevo más de 15 años trabajando con sistemas neumáticos en Bepto, y he visto de primera mano cómo la comprensión de estas ecuaciones básicas puede ahorrar miles de dólares en tiempos de inactividad y evitar costosos errores de diseño.
Índice
- Derivación de la ecuación de los gases: ¿Por qué PV = nRT es importante en los sistemas neumáticos?
- ¿Cómo se relacionan la fuerza, la presión y el área en los cilindros neumáticos?
- ¿Cuál es la relación entre caudal y velocidad en los sistemas neumáticos?
- Conclusión
- Preguntas frecuentes sobre ecuaciones de transmisión neumática
Derivación de la ecuación de los gases: ¿Por qué PV = nRT es importante en los sistemas neumáticos?
A la hora de diseñar sistemas neumáticos, es fundamental saber cómo se comportan los gases en distintas condiciones. Este conocimiento puede suponer la diferencia entre un sistema que funciona de forma fiable y otro que falla inesperadamente.
La ley de los gases ideales (PV = nRT) es fundamental para los sistemas neumáticos porque describe cómo interactúan la presión, el volumen y la temperatura. Esta relación ayuda a los ingenieros a predecir cómo se comportará el aire en cilindros sin vástago y otros componentes neumáticos en distintas condiciones de funcionamiento.
La ley de los gases ideales puede parecer un concepto teórico de las clases de física, pero tiene aplicaciones prácticas directas en los sistemas neumáticos. Permítanme explicarlo en términos más prácticos.
Comprensión de las variables en PV = nRT
| Variable | Significado | Aplicación neumática |
|---|---|---|
| P | Presión | Presión de funcionamiento de su sistema |
| V | Volumen | Tamaño de la cámara de aire en cilindros |
| n | Número de moles | Cantidad de aire en el sistema |
| R | Constante de gas2 | Constante universal (8,314 J/mol-K) |
| T | Temperatura | Temperatura de funcionamiento |
Cómo afecta la temperatura al rendimiento neumático
Las variaciones de temperatura pueden afectar considerablemente al rendimiento de los sistemas neumáticos. El año pasado, Hans, uno de nuestros clientes en Alemania, se puso en contacto conmigo porque su sistema de cilindros sin vástago no funcionaba correctamente. El sistema funcionaba perfectamente por la mañana, pero perdía potencia por la tarde.
Tras analizar su configuración, descubrimos que el sistema estaba expuesto a la luz solar directa, lo que provocaba un aumento de temperatura de 15 ºC. Utilizando la ley de los gases ideales, calculamos que este cambio de temperatura estaba provocando una variación de presión de casi 5%. Instalamos el aislamiento adecuado y el problema se resolvió de inmediato.
Aplicaciones prácticas de la ley de los gases en el diseño neumático
Al diseñar sistemas neumáticos con cilindros sin vástagola ley de los gases nos ayuda:
- Calcular los cambios de presión debidos a las fluctuaciones de temperatura
- Determinar las necesidades de volumen de los depósitos de aire
- Predecir las variaciones de la fuerza de salida en diferentes condiciones
- Dimensionar los compresores en función de la aplicación
¿Cómo se relacionan la fuerza, la presión y el área en los cilindros neumáticos?
Comprender la relación entre fuerza, presión y área es esencial a la hora de seleccionar el cilindro sin vástago adecuado para su aplicación. Este conocimiento le garantiza que obtendrá el rendimiento que necesita sin gastar de más.
En relación fuerza-presión-área3 en cilindros neumáticos se define por F = P × A, donde F es la fuerza (N), P es la presión (Pa) y A es el área efectiva (m²). Esta ecuación permite a los ingenieros calcular la fuerza exacta de salida de los cilindros sin vástago a diferentes presiones de funcionamiento.
Esta sencilla ecuación es la base de todos los cálculos de fuerza neumática, pero hay varias consideraciones prácticas que muchos ingenieros pasan por alto.
Cálculos del área efectiva para distintos tipos de cilindros
El área efectiva varía en función del tipo de cilindro:
| Tipo de cilindro | Cálculo del área efectiva | Notas |
|---|---|---|
| Acción simple | A = πr² | Área de perforación completa |
| Doble efecto (extensión) | A = πr² | Área de perforación completa |
| Doble efecto (retracción) | A = π(r² - r'²) | r' es el radio de la varilla |
| Cilindro sin vástago | A = πr² | Coherente en ambas direcciones |
Factores de eficacia de la fuerza en el mundo real
En la práctica, la salida de fuerza real se ve afectada por:
- Pérdidas por fricción: Normalmente 3-20% dependiendo del diseño de la junta
- Caídas de presión: Puede reducir la presión efectiva en 5-10%
- Efectos dinámicos: Las fuerzas de aceleración pueden reducir la fuerza disponible
Recuerdo haber trabajado con Sarah, una ingeniera mecánica de una empresa de envasado del Reino Unido. Estaba diseñando una nueva máquina y había calculado que necesitaba un cilindro sin vástago con un diámetro interior de 63 mm para conseguir la fuerza necesaria. Sin embargo, no había tenido en cuenta las pérdidas por fricción.
Recomendamos cambiar a un cilindro de 80 mm de diámetro, que proporcionó suficiente fuerza adicional para superar la fricción y mantener el rendimiento requerido. Este sencillo ajuste le ahorró un costoso rediseño tras la instalación.
Comparación de la fuerza teórica con la real
Al seleccionar cilindros sin vástago, siempre recomiendo:
- Calcular la fuerza teórica mediante F = P × A
- Aplique un factor de seguridad de 25% para la mayoría de las aplicaciones
- Verifique los cálculos con los datos de rendimiento reales del fabricante.
- Considerar las condiciones de carga dinámica si procede
¿Cuál es la relación entre caudal y velocidad en los sistemas neumáticos?
El caudal y la velocidad son parámetros críticos que determinan la rapidez de respuesta de su sistema neumático. Comprender esta relación ayuda a evitar un rendimiento lento y garantiza que el sistema cumpla los requisitos de tiempo de ciclo.
La relación entre caudal (Q) y velocidad (v)4 en sistemas neumáticos se define por Q = v × A, donde Q es el caudal volumétrico, v es la velocidad del aire y A es el área de la sección transversal del paso. Esta ecuación es crucial para dimensionar correctamente los conductos de aire y las válvulas.
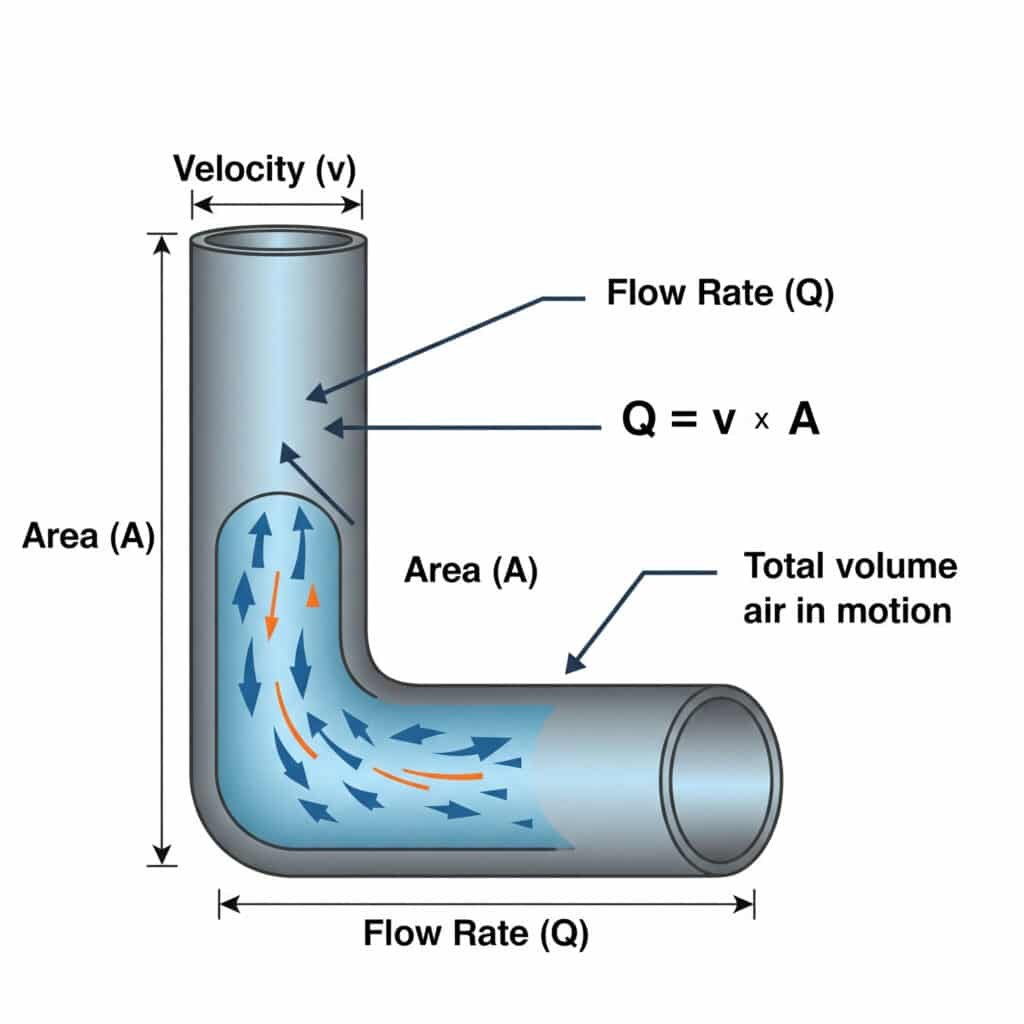
Muchos problemas de los sistemas neumáticos se derivan de un dimensionamiento inadecuado de los componentes de suministro de aire. Veamos cómo afecta esta ecuación al rendimiento en el mundo real.
Caudales críticos para componentes neumáticos comunes
Los distintos componentes tienen necesidades de caudal diferentes:
| Componente | Caudal típico requerido | Impacto del subdimensionamiento |
|---|---|---|
| Cilindro sin vástago (diámetro 25 mm) | 15-30 L/min | Funcionamiento lento, fuerza reducida |
| Cilindro sin vástago (diámetro 63 mm) | 60-120 L/min | Movimiento incoherente |
| Válvula de control direccional | Varía según el tamaño | Caída de presión, respuesta lenta |
| Unidad de preparación de aire | Total del sistema + 30% | Fluctuaciones de presión |
Cómo afecta el diámetro de las tuberías al rendimiento del sistema
El diámetro de los conductos de aire influye enormemente en el rendimiento del sistema:
- Caída de presión: Aumenta con el cuadrado de la velocidad
- Tiempo de respuesta: Líneas más pequeñas significan mayor velocidad pero más resistencia
- Eficiencia energética: Los conductos más grandes reducen la caída de presión pero aumentan el coste
Cálculo del tamaño adecuado de las líneas de los sistemas neumáticos
Para dimensionar correctamente los conductos de aire para su aplicación de cilindro sin vástago:
- Determinar el caudal necesario en función del tamaño del cilindro y la duración del ciclo
- Calcular la caída de presión máxima admisible (normalmente 0,1 bar o menos).
- Seleccione un diámetro de línea que mantenga la velocidad por debajo de 15-20 m/s
- Verificar la capacidad de flujo de la válvula (Valor Cv o Kv5) coincide con los requisitos del sistema
Una vez ayudé a un cliente en Francia que experimentaba un movimiento lento del cilindro a pesar de tener un compresor grande. El problema no era la generación insuficiente de aire, sino que los tubos de 6 mm creaban una resistencia excesiva. El cambio a tuberías de 10 mm solucionó el problema de inmediato y aumentó la frecuencia de ciclo de la máquina en 40%.
Conclusión
La comprensión de estas tres ecuaciones neumáticas fundamentales -la ley del gas ideal, la relación fuerza-presión-área y la conexión caudal-velocidad- proporciona la base para un diseño satisfactorio del sistema neumático. Aplicando estos principios, podrá seleccionar los componentes adecuados para los cilindros sin vástago, solucionar problemas de forma eficaz y optimizar el rendimiento del sistema.
Preguntas frecuentes sobre ecuaciones de transmisión neumática
¿Qué es la ley de los gases ideales y por qué es importante para los sistemas neumáticos?
La ley de los gases ideales (PV = nRT) describe cómo se relacionan la presión, el volumen, la temperatura y la cantidad de gas en un sistema neumático. Es importante porque ayuda a los ingenieros a predecir cómo afectarán las condiciones cambiantes (especialmente la temperatura) al rendimiento del sistema y a los requisitos de presión.
¿Cómo se calcula la fuerza de salida de un cilindro sin vástago?
Calcule la fuerza de salida multiplicando la presión por el área efectiva (F = P × A). Para un cilindro sin vástago, el área efectiva es la misma en ambas direcciones, lo que simplifica el cálculo de la fuerza en comparación con los cilindros convencionales que tienen fuerzas de extensión y retracción diferentes.
¿Cuál es la diferencia entre caudal y velocidad en los sistemas neumáticos?
El caudal es el volumen de aire que se mueve a través de un sistema por unidad de tiempo (normalmente en L/min), mientras que la velocidad es la rapidez con la que el aire se mueve a través de un conducto (en m/s). Se relacionan mediante la ecuación Q = v × A, donde A es el área de la sección transversal del conducto.
¿Cómo afecta la temperatura al rendimiento de los sistemas neumáticos?
La temperatura afecta directamente a la presión según la ley de los gases ideales. Un aumento de 10 °C en la temperatura puede aumentar la presión en aproximadamente 3,5% si el volumen permanece constante. Esto puede provocar variaciones de presión, afectar al rendimiento de la junta y modificar la fuerza de salida en cilindros sin vástago.
¿Cuál es la causa más común de caída de presión en los sistemas neumáticos?
Las causas más comunes de la caída de presión son los conductos de aire subdimensionados, los racores restrictivos y la capacidad de caudal inadecuada de las válvulas. Según la ecuación del caudal, los pasos más pequeños requieren una mayor velocidad del aire, lo que aumenta exponencialmente la resistencia y la caída de presión.
¿Cómo se dimensionan correctamente los conductos de aire para un cilindro sin vástago?
Dimensione los conductos de aire calculando el caudal necesario en función del volumen del cilindro y el tiempo de ciclo; a continuación, seleccione un diámetro de conducto que mantenga la velocidad del aire por debajo de 15-20 m/s para minimizar la caída de presión. Para la mayoría de las aplicaciones de cilindros sin vástago, los conductos de 8-12 mm ofrecen un buen equilibrio entre rendimiento y coste.
-
Proporciona una explicación detallada de la ley de los gases ideales, la ecuación de estado fundamental para un gas ideal hipotético que aproxima el comportamiento de muchos gases en diversas condiciones. ↩
-
Explica el papel y el valor de la constante universal de los gases (R) en la ley de los gases ideales, que sirve como constante física que relaciona las escalas de energía con las de temperatura. ↩
-
Ofrece una explicación básica de la presión, definida como la fuerza aplicada perpendicularmente a la superficie de un objeto por unidad de superficie sobre la que se distribuye dicha fuerza. ↩
-
Detalla el principio de la ecuación de continuidad, un concepto fundamental de la dinámica de fluidos que establece que, para un fluido incompresible, el caudal másico debe ser constante de una sección transversal de una tubería a otra. ↩
-
Proporciona una definición técnica del coeficiente de caudal (Cv) y del factor de caudal (Kv), que son valores normalizados utilizados para comparar las capacidades de caudal de diferentes válvulas. ↩
English 
Deutsch 
Français 
Italiano 
Español 
Português 
Русский 
العربية 
日本語 
한국어 
Bahasa Indonesia 
Türkçe 
Nederlands 
Ελληνικά 
Български 
Čeština 
Dansk 
Eesti 
Suomi 
Magyar 
Lietuvių kalba 
Latviešu valoda 
Polski 
Română 
Svenska 
Slovenčina 
Slovenščina 
Norsk bokmål 
Українська