Are you constantly struggling with pneumatic system calculations? Many engineers face the same problem when designing or troubleshooting pneumatic systems. The good news is that mastering a few key equations can solve most of your pneumatic challenges.
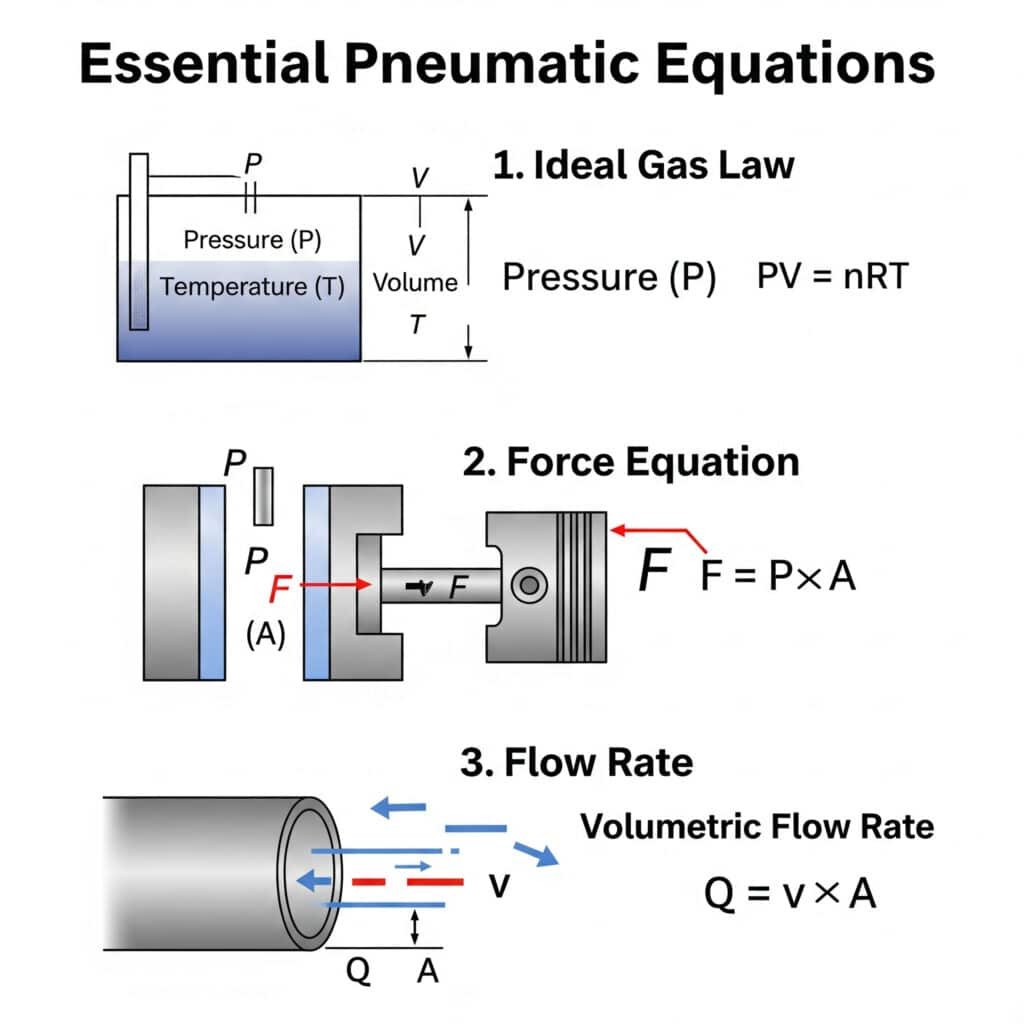
The essential pneumatic transmission equations every engineer should know include the ideal gas law (PV = nRT)1, force equation (F = P × A), and flow rate relationship (Q = v × A). Understanding these fundamentals allows for accurate system design and troubleshooting.
I’ve spent over 15 years working with pneumatic systems at Bepto, and I’ve seen firsthand how understanding these basic equations can save thousands of dollars in downtime and prevent costly design errors.
Índice
- Gas Equation Derivation: Why Does PV = nRT Matter in Pneumatic Systems?
- How Do Force, Pressure, and Area Relate in Pneumatic Cylinders?
- What’s the Relationship Between Flow Rate and Velocity in Pneumatic Systems?
- Conclusión
- FAQs About Pneumatic Transmission Equations
Gas Equation Derivation: Why Does PV = nRT Matter in Pneumatic Systems?
When designing pneumatic systems, understanding how gases behave under different conditions is crucial. This knowledge can mean the difference between a system that works reliably and one that fails unexpectedly.
The ideal gas law (PV = nRT) is fundamental to pneumatic systems because it describes how pressure, volume, and temperature interact. This relationship helps engineers predict how air will behave in rodless cylinders and other pneumatic components under varying operating conditions.

The ideal gas law might seem like a theoretical concept from physics class, but it has direct practical applications in pneumatic systems. Let me break this down into more practical terms.
Understanding the Variables in PV = nRT
| Variable | Meaning | Pneumatic Application |
|---|---|---|
| P | Presión | Operating pressure in your system |
| V | Volume | Air chamber size in cylinders |
| n | Number of moles | Amount of air in the system |
| R | Gas constant2 | Universal constant (8.314 J/mol·K) |
| T | Temperatura | Operating temperature |
How Temperature Affects Pneumatic Performance
Temperature variations can significantly impact pneumatic system performance. Last year, one of our customers in Germany, Hans, contacted me about inconsistent performance in his rodless cylinder system. The system worked perfectly in the morning but lost power in the afternoon.
After analyzing his setup, we discovered the system was exposed to direct sunlight, causing a 15°C temperature increase. Using the ideal gas law, we calculated that this temperature change was causing a pressure variation of nearly 5%. We installed proper insulation, and the problem was resolved immediately.
Practical Applications of the Gas Law in Pneumatic Design
When designing pneumatic systems with cilindros sin vástago, the gas law helps us:
- Calculate pressure changes due to temperature fluctuations
- Determine volume requirements for air reservoirs
- Predict force output variations under different conditions
- Size compressors appropriately for the application
How Do Force, Pressure, and Area Relate in Pneumatic Cylinders?
Understanding the relationship between force, pressure, and area is essential when selecting the right rodless cylinder for your application. This knowledge ensures you get the performance you need without overspending.
En force-pressure-area relationship3 in pneumatic cylinders is defined by F = P × A, where F is force (N), P is pressure (Pa), and A is the effective area (m²). This equation allows engineers to calculate the exact force output of rodless cylinders at different operating pressures.
This simple equation is the foundation of all pneumatic force calculations, but there are several practical considerations that many engineers overlook.
Effective Area Calculations for Different Cylinder Types
The effective area varies depending on the cylinder type:
| Cylinder Type | Effective Area Calculation | Notes |
|---|---|---|
| Single-acting | A = πr² | Full bore area |
| Double-acting (extension) | A = πr² | Full bore area |
| Double-acting (retraction) | A = π(r² – r’²) | r’ is rod radius |
| Rodless cylinder | A = πr² | Consistent in both directions |
Real-World Force Efficiency Factors
In practice, the actual force output is affected by:
- Friction losses: Typically 3-20% depending on seal design
- Pressure drops: Can reduce effective pressure by 5-10%
- Dynamic effects: Acceleration forces can reduce available force
I remember working with Sarah, a mechanical engineer from a packaging company in the UK. She was designing a new machine and had calculated she needed a rodless cylinder with a 63mm bore to achieve the required force. However, she hadn’t accounted for friction losses.
We recommended increasing to a 80mm bore cylinder, which provided enough additional force to overcome the friction while maintaining her required performance. This simple adjustment saved her from a costly redesign after installation.
Comparing Theoretical vs. Actual Force Output
When selecting rodless cylinders, I always recommend:
- Calculate theoretical force using F = P × A
- Apply a safety factor of 25% for most applications
- Verify calculations with actual performance data from manufacturer
- Consider dynamic loading conditions if applicable
What’s the Relationship Between Flow Rate and Velocity in Pneumatic Systems?
Flow rate and velocity are critical parameters that determine how quickly your pneumatic system responds. Understanding this relationship helps prevent sluggish performance and ensures your system meets cycle time requirements.
The relationship between flow rate (Q) and velocity (v)4 in pneumatic systems is defined by Q = v × A, where Q is the volumetric flow rate, v is the air velocity, and A is the cross-sectional area of the passage. This equation is crucial for sizing air lines and valves properly.
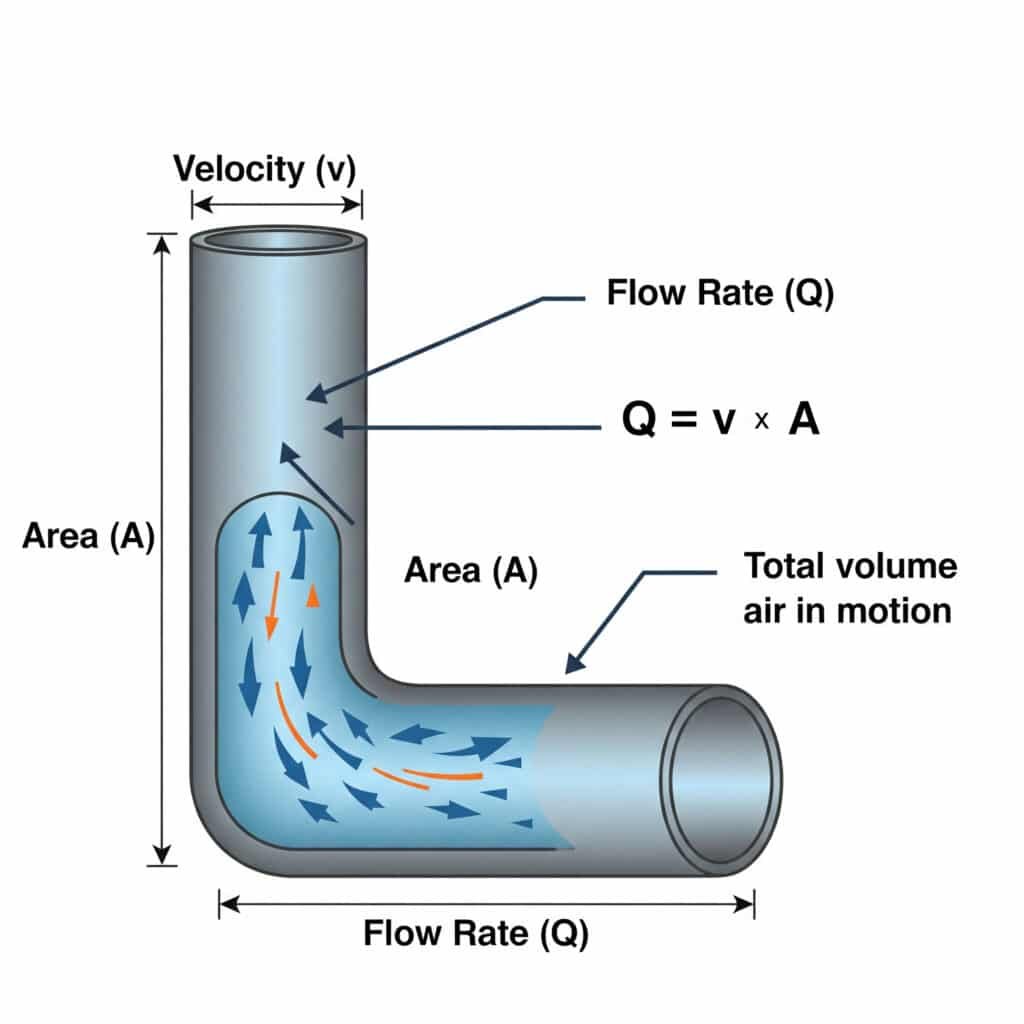
Many pneumatic system issues stem from improper sizing of air supply components. Let’s explore how this equation impacts real-world performance.
Critical Flow Rates for Common Pneumatic Components
Different components have different flow requirements:
| Componente | Typical Flow Rate Requirement | Impact of Undersizing |
|---|---|---|
| Rodless cylinder (25mm bore) | 15-30 L/min | Slow operation, reduced force |
| Rodless cylinder (63mm bore) | 60-120 L/min | Inconsistent movement |
| Directional control valve | Varies by size | Pressure drop, slow response |
| Air preparation unit | System total + 30% | Pressure fluctuations |
How Pipe Diameter Affects System Performance
The diameter of your air lines has a dramatic effect on system performance:
- Pressure drop: Increases with the square of velocity
- Response time: Smaller lines mean higher velocity but more resistance
- Energy efficiency: Larger lines reduce pressure drop but increase cost
Calculating Proper Line Sizes for Pneumatic Systems
To properly size air lines for your rodless cylinder application:
- Determine the required flow rate based on cylinder size and cycle time
- Calculate the maximum allowable pressure drop (typically 0.1 bar or less)
- Select line diameter that maintains velocity below 15-20 m/s
- Verify valve flow capacity (Cv or Kv value5) matches system requirements
I once helped a customer in France who was experiencing slow cylinder movement despite having a large compressor. The issue wasn’t insufficient air generation—it was that his 6mm tubing was creating excessive resistance. Upgrading to 10mm lines solved the problem immediately, increasing his machine’s cycle rate by 40%.
Conclusión
Understanding these three fundamental pneumatic equations—the ideal gas law, force-pressure-area relationship, and flow rate-velocity connection—provides the foundation for successful pneumatic system design. By applying these principles, you can select the right rodless cylinder components, troubleshoot issues effectively, and optimize system performance.
FAQs About Pneumatic Transmission Equations
What is the ideal gas law and why is it important for pneumatic systems?
The ideal gas law (PV = nRT) describes how pressure, volume, temperature, and gas quantity relate in a pneumatic system. It’s important because it helps engineers predict how changing conditions (especially temperature) will affect system performance and pressure requirements.
How do I calculate the force output of a rodless cylinder?
Calculate force output by multiplying the pressure by the effective area (F = P × A). For a rodless cylinder, the effective area is the same in both directions, making force calculations simpler than with conventional cylinders that have different extension and retraction forces.
What’s the difference between flow rate and velocity in pneumatic systems?
Flow rate is the volume of air moving through a system per unit time (typically in L/min), while velocity is the speed at which air moves through a passage (in m/s). They’re related by the equation Q = v × A, where A is the cross-sectional area of the passage.
How does temperature affect pneumatic system performance?
Temperature directly affects pressure according to the ideal gas law. A 10°C increase in temperature can increase pressure by approximately 3.5% if volume remains constant. This can cause pressure variations, affect seal performance, and change force output in rodless cylinders.
What’s the most common cause of pressure drop in pneumatic systems?
The most common causes of pressure drop are undersized air lines, restrictive fittings, and inadequate valve flow capacity. According to the flow rate equation, smaller passages require higher air velocity, which increases resistance and pressure drop exponentially.
How do I size air lines properly for a rodless cylinder?
Size air lines by calculating the required flow rate based on cylinder volume and cycle time, then select a line diameter that keeps air velocity below 15-20 m/s to minimize pressure drop. For most rodless cylinder applications, 8-12mm lines provide a good balance of performance and cost.
-
Provides a detailed explanation of the ideal gas law, the fundamental equation of state for a hypothetical ideal gas that approximates the behavior of many gases under various conditions. ↩
-
Explains the role and value of the universal gas constant (R) in the ideal gas law, which serves as a physical constant linking energy scales with temperature scales. ↩
-
Offers a foundational explanation of pressure, defined as the force applied perpendicular to the surface of an object per unit area over which that force is distributed. ↩
-
Details the principle of the continuity equation, a fundamental concept in fluid dynamics which states that for an incompressible fluid, the mass flow rate must be constant from one cross-section of a pipe to another. ↩
-
Provides a technical definition of the Flow Coefficient (Cv) and Flow Factor (Kv), which are standardized values used to compare the flow capacities of different valves. ↩



