
Haben Sie jemals Ihre Fabrikhalle betreten und wurden von dem unverkennbaren Zischen pneumatischer Systeme überrascht? Dieses Geräusch ist nicht nur lästig, sondern steht für verschwendete Energie, potenzielle rechtliche Probleme und ein Warnzeichen für ineffizienten Betrieb.
Akustische Geräusche in pneumatischen Systemen werden durch drei Hauptmechanismen erzeugt: Gasausdehnung während der Druckentlastung, mechanische Schwingungen von Komponenten und turbulente Strömungen in Rohren und Armaturen. Das Verständnis dieser Mechanismen ermöglicht es Ingenieuren, gezielte Strategien zur Lärmminderung umzusetzen, die die Sicherheit am Arbeitsplatz verbessern, die Energieeffizienz erhöhen und die Lebensdauer der Anlagen verlängern.
Letzten Monat besuchte ich eine pharmazeutische Produktionsstätte in New Jersey, in der übermäßiger Lärm von kolbenstangenlose Zylinder zu behördlichen Bedenken führte. Das Team hatte erfolglos allgemeine Lösungen ausprobiert. Durch die Analyse der spezifischen Lärmerzeugungsmechanismen konnten wir den Lärm ihres Systems um 14 dBA reduzieren - und es damit von einem regulatorischen Risiko in einen Bereich bringen, der den Vorschriften entspricht. Lassen Sie mich Ihnen zeigen, wie wir das gemacht haben.
Inhaltsübersicht
- Schallpegel der Gasexpansion: Welche Formel sagt den Lärm von pneumatischen Auspuffanlagen voraus?
- Mechanisches Schwingungsspektrum: Wie kann die Frequenzanalyse Lärmquellen identifizieren?
- Einfügungsdämpfung von Schalldämpfern: Welche Berechnungen sind ausschlaggebend für ein effektives Schalldämpferdesign?
- Schlussfolgerung
- FAQs zum Thema Lärm in pneumatischen Systemen
Schallpegel der Gasexpansion: Welche Formel sagt den Lärm von pneumatischen Auspuffanlagen voraus?
Die plötzliche Ausdehnung der Druckluft bei der Betätigung von Ventilen oder beim Entlüften von Zylindern ist eine der wichtigsten Lärmquellen in pneumatischen Systemen. Das Verständnis der mathematischen Beziehung zwischen den Systemparametern und der Geräuschentwicklung ist für eine wirksame Lärmminderung unerlässlich.
Der Schallleistungspegel der Gasausdehnung kann mit der Formel berechnet werden: Lw = 10 log₁₀(W/W₀), wobei W die Schallleistung in Watt und W₀ die Bezugsleistung (10-¹² Watt) ist. Für pneumatische Systeme kann W als W = η × m × (c²/2) geschätzt werden, wobei η der akustische Wirkungsgrad, m der Massendurchsatz und c die Gasgeschwindigkeit ist.
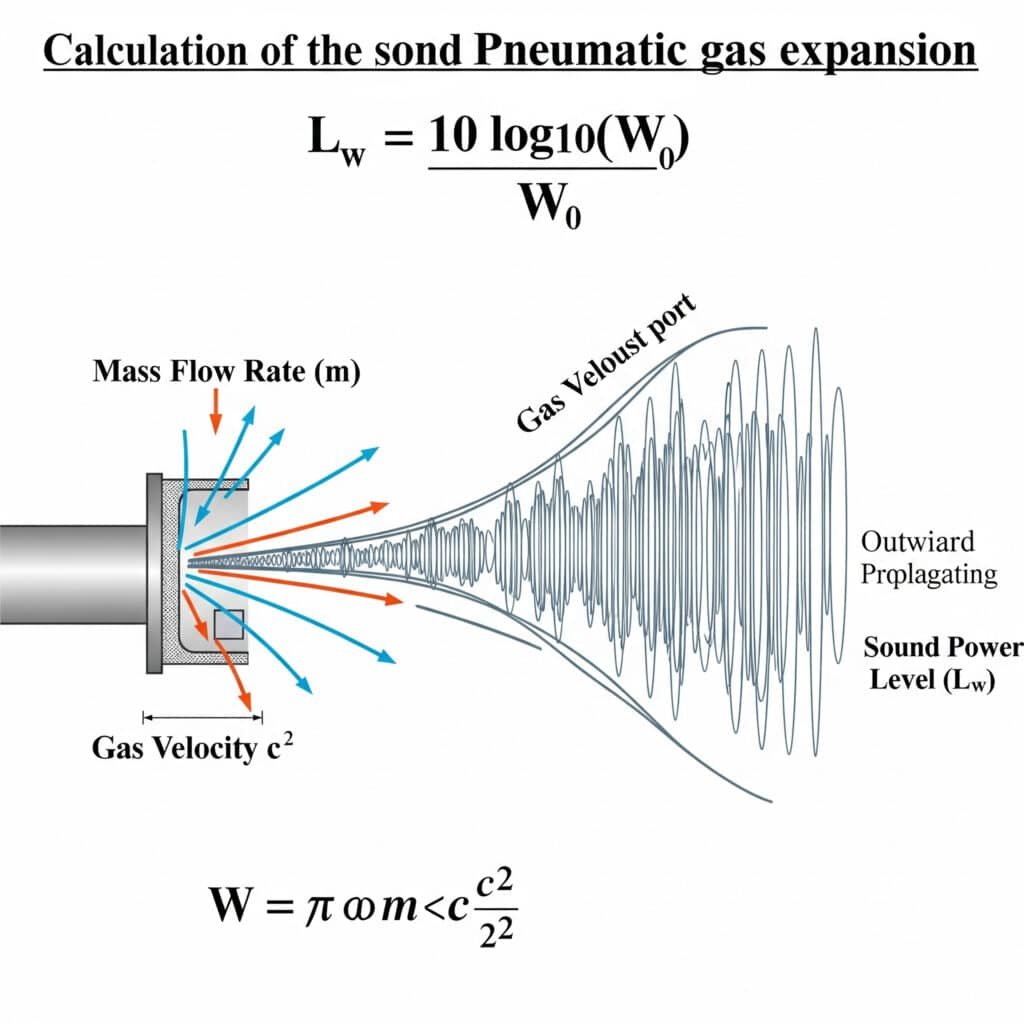
Ich erinnere mich an die Fehlersuche an einer Verpackungslinie in Illinois, wo der Lärmpegel 95 dBA überstieg - weit mehr als OSHA-Grenzwerte1. Das Wartungsteam hatte sich auf mechanische Ursachen konzentriert, aber unsere Analyse ergab, dass 70% des Lärms von den Auslassöffnungen kam. Durch Anwendung der Gasausdehnungsformel stellten wir fest, dass der Betriebsdruck um 2,2 bar höher war als erforderlich, was zu übermäßigen Abgasgeräuschen führte. Diese einfache Druckanpassung reduzierte den Lärm um 8 dBA, ohne die Leistung zu beeinträchtigen.
Grundlegende Gleichungen für das Gasausdehnungsgeräusch
Schauen wir uns die wichtigsten Formeln für die Vorhersage von Expansionslärm an:
Berechnung der Schallleistung
Die durch expandierendes Gas erzeugte Schallleistung kann wie folgt berechnet werden:
W = η × m × (c²/2)
Wo:
- W = Schallleistung (Watt)
- η = Akustischer Wirkungsgrad (typischerweise 0,001-0,01 für pneumatische Auspuffanlagen)
- m = Massendurchsatz (kg/s)
- c = Gasgeschwindigkeit am Auslass (m/s)
Der Schallleistungspegel in Dezibel ist dann:
Lw = 10 log₁₀(W/W₀)
Dabei ist W₀ die Bezugsleistung von 10-¹² Watt.
Bestimmung des Massendurchsatzes
Der Massendurchsatz durch eine Blende kann wie folgt berechnet werden:
m = Cd × A × p₁ × √(2γ/(γ-1) × (RT₁) × [(p₂/p₁)^(2/γ) - (p₂/p₁)^((γ+1)/γ)])
Wo:
- Cd = Abflusskoeffizient (normalerweise 0,6-0,8)
- A = Fläche der Blende (m²)
- p₁ = Vorgelagerter absoluter Druck (Pa)
- p₂ = absoluter Druck im Abfluss (Pa)
- γ = Spezifisches Wärmeverhältnis (1,4 für Luft)
- R = Gaskonstante für Luft (287 J/kg-K)
- T₁ = Vorlauftemperatur (K)
Bei gedrosseltem Durchfluss (häufig bei pneumatischen Abgasen) vereinfacht sich dies zu:
m = Cd × A × p₁ × √(γ/(RT₁)) × (2/(γ+1))^((γ+1)/(2(γ-1)))
Faktoren, die das Gasausdehnungsgeräusch beeinflussen
| Faktor | Auswirkungen auf den Lärmpegel | Ansatz zur Risikominderung |
|---|---|---|
| Betriebsdruck | 3-4 dBA Erhöhung pro Balken | Den Systemdruck auf das erforderliche Minimum reduzieren |
| Größe der Auslassöffnung | Kleinere Anschlüsse erhöhen Geschwindigkeit und Lärm | Verwenden Sie für die Durchflussanforderungen richtig dimensionierte Anschlüsse |
| Abgastemperatur | Höhere Temperaturen erhöhen den Lärm | Möglichst vor der Expansion abkühlen lassen |
| Ausdehnungsverhältnis | Höhere Verhältnisse erzeugen mehr Lärm | Stufenweise Erweiterung durch mehrere Schritte |
| Durchflussmenge | Verdoppelung des Durchflusses erhöht den Lärm um ~3 dBA | Verwendung mehrerer kleinerer Auspuffanlagen anstelle einer großen Anlage |
Praktisches Beispiel für Lärmvorhersage
Für einen typischen kolbenstangenlosen Zylinder mit:
- Betriebsdruck: 6 bar (600.000 Pa)
- Durchmesser der Auslassöffnung: 4 mm (Fläche = 1,26 × 10-⁵ m²)
- Entladungskoeffizient: 0,7
- Akustischer Wirkungsgrad: 0,005
Der Massendurchsatz bei der Auspuffanlage würde ungefähr betragen:
m = 0,7 × 1,26 × 10-⁵ × 600.000 × 0,0404 = 0,0214 kg/s
Bei einer Auspuffgeschwindigkeit von 343 m/s (Schallgeschwindigkeit) wäre die Schallleistung gleich:
W = 0,005 × 0,0214 × (343²/2) = 6,29 Watt
Der resultierende Schallleistungspegel:
Lw = 10 log₁₀(6,29/10-¹²) = 128 dB
Dieser hohe Schallleistungspegel erklärt, warum ungedämpfte pneumatische Auspuffanlagen in industriellen Umgebungen so bedeutende Lärmquellen sind.
Mechanisches Schwingungsspektrum: Wie kann die Frequenzanalyse Lärmquellen identifizieren?
Mechanische Schwingungen in pneumatischen Komponenten erzeugen charakteristische Geräuschsignaturen, die analysiert werden können, um spezifische Probleme zu lokalisieren. Die Analyse des Frequenzspektrums ist der Schlüssel zur Identifizierung und Behebung dieser mechanischen Geräuschquellen.
Mechanische Schwingungen in pneumatischen Systemen erzeugen Geräusche mit charakteristischen Frequenzspektren, die mit Hilfe der folgenden Methoden analysiert werden können Schnelle Fourier-Transformation (FFT)2 Techniken. Zu den wichtigsten Frequenzbereichen gehören niederfrequente Strukturschwingungen (10-100 Hz), mittelfrequente Betriebsharmonische (100-1000 Hz) und hochfrequente strömungsinduzierte Schwingungen (1-10 kHz), die jeweils unterschiedliche Minderungsmaßnahmen erfordern.
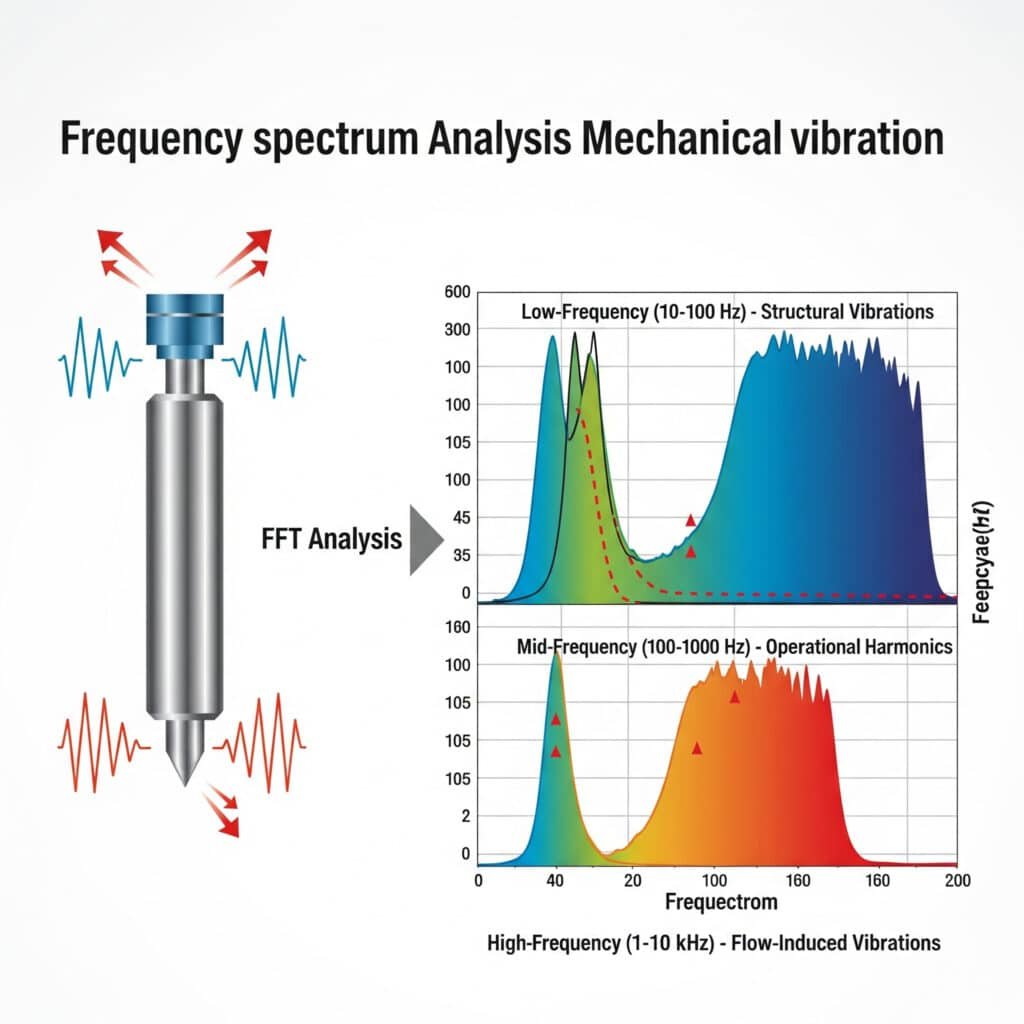
Während eines Beratungsgesprächs bei einem Automobilzulieferer in Michigan kämpfte das Wartungsteam mit übermäßigen Geräuschen aus einem kolbenstangenlosen Zylindertransfersystem. Die konventionelle Fehlersuche konnte die Quelle nicht identifizieren. Unsere Analyse des Schwingungsspektrums ergab eine deutliche Spitze bei 237 Hz - genau passend zur internen Dichtbandresonanz des Zylinders. Durch eine Änderung des Montagesystems zur Dämpfung dieser spezifischen Frequenz konnten wir den Lärm ohne Produktionsunterbrechung um 11 dBA reduzieren.
Methodik der Frequenzspektrumsanalyse
Eine wirksame Schwingungsanalyse folgt einem systematischen Ansatz:
- Messaufbau: Verwendung von Beschleunigungsmessern und akustischen Mikrofonen
- Datenerfassung: Erfassung von Schwingungssignalen im Zeitbereich
- FFT-Analyse: Umwandlung in den Frequenzbereich
- Spektrales Mapping: Identifizierung charakteristischer Frequenzen
- Quelle Zuschreibung: Zuordnung von Frequenzen zu bestimmten Komponenten
Charakteristische Frequenzbereiche in pneumatischen Systemen
| Frequenzbereich | Typische Quellen | Akustische Merkmale |
|---|---|---|
| 10-50 Hz | Strukturelle Resonanz, Montageprobleme | Niederfrequentes Rumpeln, mehr gefühlt als gehört |
| 50-200 Hz | Kolbenstöße, Ventilbetätigung | Deutliches Pochen oder Klopfen |
| 200-500 Hz | Dichtungsreibung, interne Resonanz | Mittelfrequentes Summen oder Brummen |
| 500-2000 Hz | Strömungsturbulenzen, Druckpulsationen | Zischen mit tonalen Komponenten |
| 2-10 kHz | Leckage, Hochgeschwindigkeitsströmung | Scharfes Zischen, sehr störend für das menschliche Ohr |
| >10 kHz | Mikroturbulenz, Gasausdehnung | Ultraschallkomponenten, Energieverlustanzeige |
Wege der Schwingungsübertragung
Lärm durch mechanische Schwingungen entsteht auf mehreren Wegen:
Übertragung über die Struktur
Schwingungen wandern durch feste Bauteile:
- Bauteil schwingt durch innere Kräfte
- Schwingungsübertragung durch Befestigungspunkte
- Verbundene Strukturen verstärken den Schall und strahlen ihn ab
- Große Flächen wirken als effiziente Schallstrahler
Übertragung aus der Luft
Direkte Abstrahlung von Schall von vibrierenden Oberflächen:
- Oberflächenvibration verdrängt Luft
- Verdrängung erzeugt Druckwellen
- Wellen breiten sich in der Luft aus
- Größe der Strahlungsfläche bestimmt den Wirkungsgrad
Fallstudie: Schwingungsanalyse bei kolbenstangenlosen Zylindern
Für einen magnetischen kolbenstangenlosen Zylinder, der übermäßige Geräusche verursacht:
| Frequenz (Hz) | Amplitude (dB) | Identifizierung der Quelle | Strategie zur Risikominderung |
|---|---|---|---|
| 43 | 78 | Montage-Resonanz | Versteifte Halterung |
| 86 | 65 | Harmonische der Befestigungsresonanz | Angesprochen mit primärer Resonanz |
| 237 | 91 | Siegelbandresonanz | Dämpfungsmaterial zum Zylinderkörper hinzugefügt |
| 474 | 83 | Harmonische des Dichtungsbandes | Angesprochen mit primärer Resonanz |
| 1250 | 72 | Turbulenzen im Luftstrom | Geänderte Hafengestaltung |
| 3700 | 68 | Leckage an Endkappen | Ersetzte Dichtungen |
Die kombinierten Minderungsstrategien reduzierten den Gesamtlärm um 14 dBA, wobei die größte Verbesserung durch die Behebung der 237-Hz-Resonanz erzielt wurde.
Fortgeschrittene Techniken der Schwingungsanalyse
Neben der grundlegenden FFT-Analyse bieten verschiedene fortgeschrittene Techniken tiefere Einblicke:
Auftragsanalyse
Besonders nützlich für Systeme mit variabler Drehzahl:
- Verfolgt Frequenzen, die mit der Betriebsgeschwindigkeit skalieren
- Trennt drehzahlabhängige von festfrequenten Komponenten
- Identifiziert Probleme im Zusammenhang mit bestimmten Bewegungsphasen
Analyse der Betriebsablenkungsform (ODS)
Kartiert Schwingungsmuster im gesamten System:
- Mehrere Messpunkte erzeugen eine "Schwingungskarte".
- Zeigt, wie sich Strukturen während des Betriebs bewegen
- Identifiziert optimale Stellen für Dämpfungsmaßnahmen
Modalanalyse
Ermittelt Eigenfrequenzen und Eigenformen:
- Identifiziert Resonanzfrequenzen vor dem Betrieb
- Prognostiziert potenzielle Problemhäufigkeiten
- Leitet strukturelle Änderungen zur Vermeidung von Resonanz
Einfügungsdämpfung von Schalldämpfern: Welche Berechnungen sind ausschlaggebend für ein effektives Schalldämpferdesign?
Schalldämpfer und Schalldämpfer sind von entscheidender Bedeutung für die Geräuschreduzierung in pneumatischen Systemen, aber ihre Konstruktion muss auf soliden technischen Berechnungen beruhen, um die Wirksamkeit zu gewährleisten, ohne die Systemleistung zu beeinträchtigen.
Auspufftopf Einfügungsdämpfung3 (IL) quantifiziert die Wirksamkeit der Lärmminderung und kann berechnet werden als IL = Lw₁ - Lw₂, wobei Lw₁ der Schallleistungspegel ohne Schalldämpfer und Lw₂ der Pegel mit installiertem Schalldämpfer ist. Bei pneumatischen Systemen erreichen wirksame Schalldämpfer in der Regel eine Einfügungsdämpfung von 15-30 dB im kritischen Frequenzbereich von 500 Hz bis 4 kHz, wobei ein akzeptabler Gegendruck erhalten bleibt.
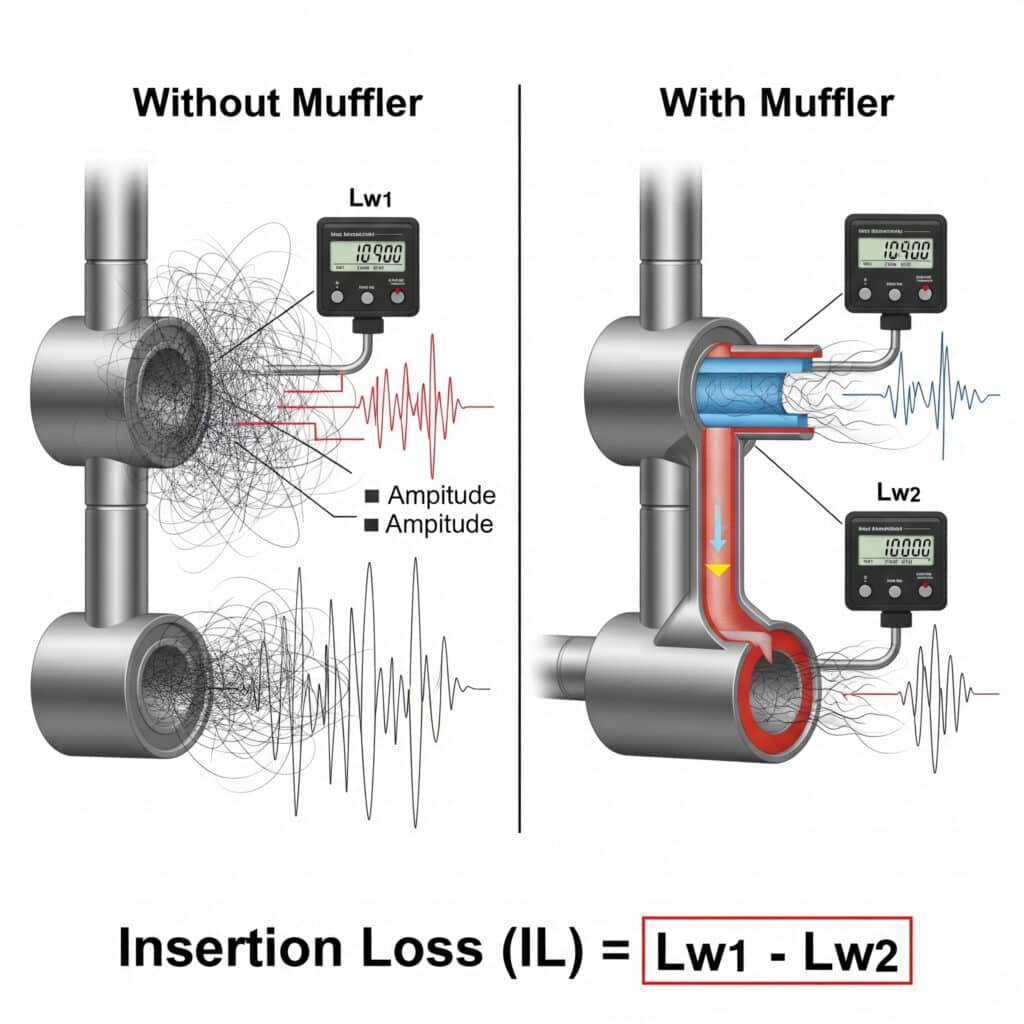
Vor kurzem habe ich einem Hersteller medizinischer Geräte in Massachusetts geholfen, ein schwieriges Lärmproblem mit seinem kolbenstangenlosen Präzisionszylindersystem zu lösen. Der anfängliche Versuch, Schalldämpfer von der Stange zu verwenden, reduzierte zwar den Lärm, erzeugte aber einen übermäßigen Gegendruck, der die Zykluszeiten beeinträchtigte. Durch die Berechnung der erforderlichen Einfügungsdämpfung für bestimmte Frequenzbänder und die Entwicklung eines kundenspezifischen Mehrkammerschalldämpfers erreichten wir eine Geräuschreduzierung von 24 dB bei minimaler Leistungsbeeinträchtigung. Das Ergebnis war ein System, das sowohl die Geräusch- als auch die Präzisionsanforderungen des Unternehmens erfüllte.
Grundlagen der Einfügungsdämpfung von Schalldämpfern
Die Kerngleichung für die Einfügungsdämpfung lautet:
IL = Lw₁ - Lw₂
Wo:
- IL = Einfügungsdämpfung (dB)
- Lw₁ = Schallleistungspegel ohne Schalldämpfer (dB)
- Lw₂ = Schallleistungspegel mit Schalldämpfer (dB)
Für die frequenzspezifische Analyse wird dies zu:
IL(f) = Lw₁(f) - Lw₂(f)
Dabei bezeichnet f das zu analysierende Frequenzband.
Konstruktionsparameter von Schalldämpfern und ihre Auswirkungen
| Parameter | Auswirkung auf die Einfügedämpfung | Wirkung auf den Gegendruck | Optimale Reichweite |
|---|---|---|---|
| Volumen der Kammer | Größere Lautstärke erhöht IL bei niedrigen Frequenzen | Minimale Auswirkungen bei richtiger Planung | 10-30× Volumen der Auslassöffnung |
| Anzahl der Kammern | Mehr Kammern erhöhen die IL im mittleren Frequenzbereich | Steigt mit mehr Kammern | 2-4 Kammern für die meisten Anwendungen |
| Ausdehnungsverhältnis | Höhere Quoten verbessern IL | Minimale Auswirkungen bei schrittweiser Umsetzung | Flächenverhältnis 4:1 bis 16:1 |
| Akustisches Material | Verbessert hochfrequente IL | Minimale Auswirkungen bei richtiger Gestaltung | 10-50 mm Dicke |
| Luftleitblech Perforation | Beeinflusst mittlere Frequenzen IL | Erhebliche Auswirkungen | 30-50% offene Fläche |
| Länge der Fließwege | Längere Pfade verbessern IL bei niedrigen Frequenzen | Nimmt mit der Länge zu | 3-10× Öffnungsdurchmesser |
Theoretische Modelle zur Vorhersage der Einfügedämpfung
Mehrere Modelle können die Einfügungsdämpfung für verschiedene Schalldämpfertypen vorhersagen:
Modell der Expansionskammer
Für einfache Expansionskammern:
IL = 10 log₁₀[1 + 0,25(m-1/m)² sin²(kL)]
Wo:
- m = Flächenverhältnis (Kammerfläche / Rohrfläche)
- k = Wellenzahl (2πf/c, wobei f die Frequenz und c die Schallgeschwindigkeit ist)
- L = Länge der Kammer
Dissipativ-Schalldämpfer Modell
Für Schalldämpfer mit schallabsorbierenden Materialien:
IL = 8,68α(L/d)
Wo:
- α = Absorptionskoeffizient des Materials
- L = Länge des ausgekleideten Abschnitts
- d = Durchmesser des Fließweges
Reaktiver Schalldämpfer Modell (Helmholtz-Resonator4)
Für Resonator-Schalldämpfer:
IL = 10 log₁₀[1 + (ρc/2S)² × (V/L'c²) × ω²/((ω₀² - ω²)² + (Rω/ρc)²)]
Wo:
- ρ = Luftdichte
- c = Schallgeschwindigkeit
- S = Querschnittsfläche des Halses
- V = Volumen des Hohlraums
- L' = Effektive Halslänge
- ω = Winkelfrequenz
- ω₀ = Resonanzfrequenz
- R = Akustischer Widerstand
Praktischer Schalldämpfer-Auswahlprozess
Auswahl oder Konstruktion eines geeigneten Schalldämpfers:
- Messung des Rauschspektrums: Frequenzgehalt des Lärms bestimmen
- Erforderliche IL berechnen: Erforderliche Reduktion nach Häufigkeit bestimmen
- Bewertung der Flussanforderungen: Berechnung des maximal zulässigen Gegendrucks
- Schalldämpfertyp auswählen:
- Reaktiv (Expansionskammern) für niedrige Frequenzen
- Dissipativ (absorptiv) für hohe Frequenzen
- Kombination für breitbandigen Lärm - Leistung überprüfen: Test Einfügungsdämpfung und Gegendruck
Gegendruck Überlegungen
Übermäßiger Gegendruck kann die Systemleistung erheblich beeinträchtigen:
Berechnung des Gegendrucks
Der Gegendruck kann geschätzt werden als:
ΔP = ρ(Q/Cd×A)²/2
Wo:
- ΔP = Druckabfall (Pa)
- ρ = Luftdichte (kg/m³)
- Q = Durchflussmenge (m³/s)
- Cd = Entladungskoeffizient
- A = Effektiver Durchflussbereich (m²)
Bewertung der Auswirkungen auf die Leistung
Für einen kolbenstangenlosen Zylinder mit:
- Bohrungsdurchmesser: 40 mm
- Hub: 500mm
- Zykluszeit: 2 Sekunden
- Betriebsdruck: 6 bar
Jeder 0,1 bar Gegendruck würde:
- Verringern Sie die Kraftausgabe um etwa 1,7%
- Erhöhung der Zykluszeit um etwa 2,3%
- Erhöhung des Energieverbrauchs um etwa 1,5%
Fallstudie: Individuelles Schalldämpferdesign
Für eine kolbenstangenlose Präzisionszylinderanwendung mit strengen Geräuschanforderungen:
| Parameter | Ausgangssituation | Auspufftopf von der Stange | Individuelles Design |
|---|---|---|---|
| Schallpegel | 89 dBA | 76 dBA | 65 dBA |
| Gegendruck | 0,05 bar | 0,42 bar | 0,11 bar |
| Zykluszeit | 1,8 Sekunden | 2,3 Sekunden | 1,9 Sekunden |
| Frequenzgang | Breitband | Schlecht bei 2-4 kHz | Optimiert über das gesamte Spektrum |
| Nutzungsdauer | K.A. | 3 Monate (Verstopfung) | >12 Monate |
| Durchführung Kosten | K.A. | $120 pro Punkt | $280 pro Punkt |
Der maßgeschneiderte Schalldämpfer sorgte für eine überragende Geräuschreduzierung bei gleichzeitig akzeptabler Systemleistung und einer Amortisationszeit von weniger als 6 Monaten, wenn man die Produktivitätssteigerung berücksichtigt.
Schlussfolgerung
Das Verständnis der Mechanismen der akustischen Lärmerzeugung - Gasausdehnungsschallpegel, mechanische Schwingungsspektren und Berechnungen der Einfügungsdämpfung von Schalldämpfern - bildet die Grundlage für eine effektive Lärmminderung in pneumatischen Systemen. Durch die Anwendung dieser Prinzipien können Sie leisere, effizientere und zuverlässigere pneumatische Systeme schaffen und gleichzeitig die Einhaltung von Vorschriften gewährleisten und die Bedingungen am Arbeitsplatz verbessern.
FAQs zum Thema Lärm in pneumatischen Systemen
Was sind die OSHA-Grenzwerte für die Lärmbelastung durch pneumatische Systeme?
Die OSHA begrenzt die Lärmbelastung am Arbeitsplatz auf 90 dBA für einen zeitlich gewichteten 8-Stunden-Mittelwert mit einer Austauschrate von 5 dBA. Der von der NIOSH empfohlene Grenzwert ist jedoch mit 85 dBA eher konservativ. Pneumatische Systeme überschreiten diese Grenzwerte häufig, da ungedämpfte Abgase oft 90-110 dBA in einem Meter Entfernung erzeugen, was technische Kontrollen zur Einhaltung der Grenzwerte erfordert.
Wie wirkt sich der Betriebsdruck auf die Geräuschentwicklung von Druckluftanlagen aus?
Der Betriebsdruck hat einen erheblichen Einfluss auf die Lärmerzeugung, wobei jeder Druckanstieg um 1 bar in der Regel den Auspuffgeräuschpegel um 3-4 dBA erhöht. Diese Beziehung ist eher logarithmisch als linear, da die Schallleistung mit dem Quadrat des Druckverhältnisses zunimmt. Die Reduzierung des Systemdrucks auf das für den Betrieb erforderliche Minimum ist oft die einfachste und kostengünstigste Strategie zur Lärmminderung.
Was ist der Unterschied zwischen reaktiven und dissipativen Schalldämpfern für pneumatische Systeme?
Reaktive Schalldämpfer verwenden Kammern und Kanäle, um Schallwellen zu reflektieren und destruktive Interferenzen zu erzeugen. Dadurch sind sie für tieffrequente Geräusche (unter 500 Hz) mit minimalem Druckverlust geeignet. Dissipative Schalldämpfer verwenden schallabsorbierende Materialien, um Schallenergie in Wärme umzuwandeln. Dadurch sind sie effektiver bei hochfrequentem Lärm (über 500 Hz), aber auch anfälliger für Verschmutzung. Viele industrielle Druckluftschalldämpfer kombinieren beide Prinzipien zur breitbandigen Lärmminderung.
Wie kann ich die vorherrschende Lärmquelle in meinem pneumatischen System identifizieren?
Gehen Sie systematisch vor und beginnen Sie mit Betriebstests: Lassen Sie das System bei verschiedenen Drücken, Geschwindigkeiten und Lasten laufen und messen Sie dabei das Geräusch. Führen Sie dann eine Komponentenisolierung durch, indem Sie einzelne Elemente separat betreiben. Führen Sie schließlich eine Frequenzanalyse mit einem oktavbandfähigen Schallpegelmesser durch - niedrige Frequenzen (50-250 Hz) weisen in der Regel auf strukturelle Probleme hin, mittlere Frequenzen (250-2000 Hz) auf Betriebsgeräusche und hohe Frequenzen (2-10 kHz) auf Strömungs- oder Leckageprobleme.
Welcher Zusammenhang besteht zwischen dem Geräuschpegel und dem Abstand zu einer pneumatischen Komponente?
Die Geräusche von pneumatischen Komponenten folgen unter Freifeldbedingungen dem umgekehrten quadratischen Gesetz, d. h. sie nehmen mit jeder Verdoppelung der Entfernung um etwa 6 dB ab. In typischen Industrieumgebungen mit reflektierenden Oberflächen beträgt die tatsächliche Verringerung jedoch aufgrund des Nachhalls oft nur 3 bis 4 dB pro Verdoppelung des Abstands. Das bedeutet, dass eine Verdoppelung des Abstands zu einer 90-dB-Lärmquelle den Pegel nur auf 86-87 dB und nicht auf die theoretischen 84 dB reduziert.
-
Enthält die offiziellen Vorschriften der Occupational Safety and Health Administration (OSHA) und die zulässigen Grenzwerte (PEL) für Lärm am Arbeitsplatz, die ein wichtiger Faktor für die Lärmminderung sind. ↩
-
Erläutert den Algorithmus der schnellen Fourier-Transformation (FFT), ein wichtiges mathematisches Werkzeug zur Umwandlung eines Zeitsignals (z. B. einer Schwingung oder Schallwelle) in seine einzelnen Frequenzkomponenten für die Analyse. ↩
-
Beschreibt die Modalanalyse, ein fortschrittliches technisches Verfahren zur Bestimmung der inhärenten dynamischen Eigenschaften eines Systems, z. B. seiner Eigenfrequenzen und Modenformen, um Resonanzen vorherzusagen und zu vermeiden. ↩
-
Bietet eine ausführliche Erläuterung der Einfügungsdämpfung (IL), der primären Messgröße zur Quantifizierung der Leistung eines Schalldämpfers oder Schalldämpfers durch Messung der von ihm erzielten Schallpegelminderung. ↩



