
Haben Sie mit ungleichmäßigen Geschwindigkeiten von Pneumatikzylindern oder unerwarteten Stößen am Ende des Hubs zu kämpfen? Diese häufigen Probleme sind häufig auf ein unzureichendes Verständnis der Kolbenkinematik zurückzuführen. Viele Ingenieure konzentrieren sich ausschließlich auf die Kraftanforderungen und übersehen dabei die kritischen Bewegungsparameter, die die Systemleistung bestimmen.
Kolben-Kinematik1 wirken sich direkt auf die Leistung pneumatischer Systeme durch Druck-Geschwindigkeits-Beziehungen, Beschleunigungsgrenzen und Dämpfungsanforderungen aus. Das Verständnis dieser Prinzipien ermöglicht es Ingenieuren, Komponenten richtig zu dimensionieren, tatsächliche Bewegungsprofile vorherzusagen und vorzeitige Ausfälle in kolbenstangenlosen Zylindern und anderen pneumatischen Aktuatoren zu verhindern.
In den mehr als 15 Jahren, in denen ich bei Bepto mit pneumatischen Systemen arbeite, habe ich unzählige Fälle erlebt, in denen das Verständnis dieser grundlegenden Prinzipien den Kunden geholfen hat, hartnäckige Leistungsprobleme zu lösen und die Lebensdauer der Anlagen um das 3-5fache zu verlängern.
Inhaltsübersicht
- Welchen Druck braucht man eigentlich für eine konstante Geschwindigkeit?
- Wie berechnet man die maximal mögliche Beschleunigung in Pneumatikzylindern?
- Warum ist die Dämpfungszeit wichtig und wie wird sie berechnet?
- Schlussfolgerung
- FAQs zur Kolbenkinematik in pneumatischen Systemen
Welchen Druck braucht man eigentlich für eine konstante Geschwindigkeit?
Viele Ingenieure wenden einfach den maximal verfügbaren Druck auf ihre pneumatischen Systeme an, aber dieser Ansatz ist ineffizient und kann zu ruckartigen Bewegungen, übermäßigem Verschleiß und Energieverschwendung führen.
Der für eine Bewegung mit konstanter Geschwindigkeit in einem Pneumatikzylinder erforderliche Druck wird mit P = (F + Fr)/A berechnet, wobei P der Druck, F die externe Lastkraft, Fr der Reibungswiderstand und A die Kolbenfläche ist. Diese Berechnung gewährleistet einen reibungslosen, effizienten Betrieb ohne übermäßigen Druck, der Energie verschwendet und den Verschleiß der Komponenten beschleunigt.
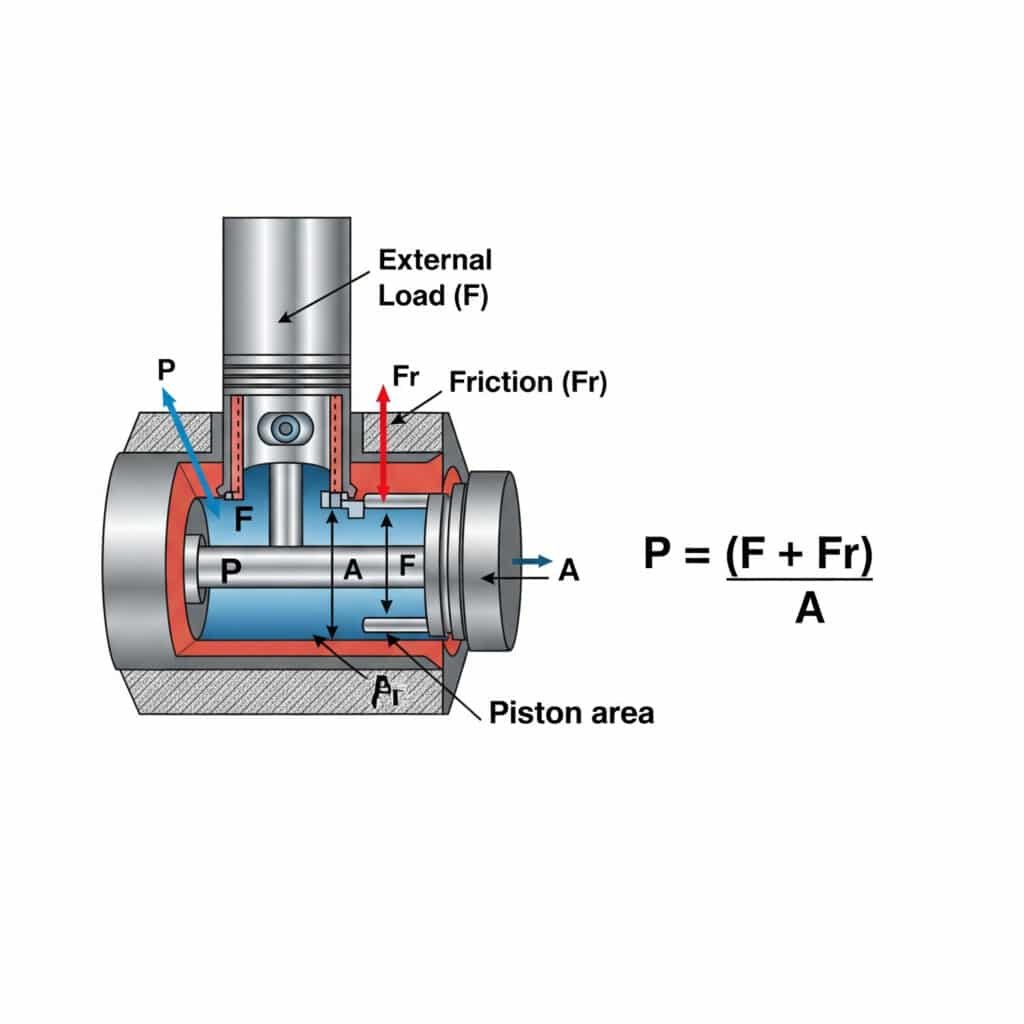
Das Verständnis der Druckanforderungen für Bewegungen mit konstanter Geschwindigkeit hat praktische Auswirkungen auf die Systemauslegung und den Betrieb. Lassen Sie mich dies in umsetzbare Erkenntnisse aufschlüsseln.
Faktoren, die die Druckanforderungen bei konstanter Geschwindigkeit beeinflussen
Der zur Aufrechterhaltung einer konstanten Geschwindigkeit erforderliche Druck hängt von mehreren Faktoren ab:
| Faktor | Auswirkung auf die Druckanforderung | Praktische Überlegungen |
|---|---|---|
| Externe Belastung | Direkte lineare Beziehung | Variiert je nach Ausrichtung und externen Kräften |
| Reibung | Erhöht den erforderlichen Druck | Veränderungen bei Dichtungsverschleiß und Schmierung |
| Kolbenbereich | Umgekehrt proportional | Größere Bohrung = geringerer Druckbedarf |
| Beschränkungen der Luftzufuhr | Druckabfall in Leitungen/Ventilen | Dimensionierung der Komponenten für minimalen Druckabfall |
| Gegendruck | Lehnt den Antrag ab | Abgasdurchsatz berücksichtigen |
Berechnung des Mindestdrucks für eine stabile Bewegung
Bestimmung des Mindestdrucks, der für eine stabile Bewegung erforderlich ist:
- Berechnen Sie die Kraft, die erforderlich ist, um die äußere Last zu überwinden
- Addieren Sie die Reibungskraft (normalerweise 3-20% der maximalen Kraft)
- Dividieren durch die effektive Kolbenfläche
- Hinzufügen eines Stabilitätsfaktors (normalerweise 10-30%)
Zum Beispiel bei einem kolbenstangenlosen Zylinder mit 40 mm Bohrung und einer Last von 10 kg und einer Reibung von 15%:
| Parameter | Berechnung | Ergebnis |
|---|---|---|
| Belastung Kraft | 10kg × 9,81m/s² | 98.1N |
| Reibungskraft | 15% der maximalen Kraft bei 6 bar | ~45N |
| Gesamtkraft | 98,1N + 45N | 143.1N |
| Kolbenbereich | π × (0,02m)² | 0.00126m² |
| Minimaler Druck | 143,1N ÷ 0,00126m² | 113.571 Pa (1,14 bar) |
| Mit 20% Stabilitätsfaktor | 1,14 bar × 1,2 | 1,37 bar |
Real-World Anwendung: Energieeinsparungen durch Druckoptimierung
Letztes Jahr arbeitete ich mit Robert, einem Produktionsingenieur in einem Möbelwerk in Michigan. Seine automatisierte Montagelinie arbeitete mit kolbenstangenlosen Zylindern, die unabhängig von der Last mit dem vollen Versorgungsdruck von 6 bar arbeiteten.
Nach der Analyse seiner Anwendung stellten wir fest, dass die meisten Bewegungen nur 2,5-3 bar für einen stabilen Betrieb benötigen. Durch den Einbau von Proportional-DruckregelventileWir haben den Luftverbrauch um 40% gesenkt, während die Zykluszeit gleich geblieben ist. Dadurch konnten wir jährlich etwa $12.000 an Energiekosten einsparen und gleichzeitig den Verschleiß der Dichtungen verringern und die Wartungsintervalle verlängern.
Verhältnis zwischen Geschwindigkeit und Druck in realen Systemen
In der Praxis ist die Beziehung zwischen Druck und Geschwindigkeit aus folgenden Gründen nicht vollkommen linear:
- Durchflussbeschränkungen: Ventil- und Anschlussgrößen beeinflussen die maximal erreichbare Geschwindigkeit
- Auswirkungen der Komprimierbarkeit: Luft ist komprimierbar und verursacht Verzögerungen bei der Beschleunigung
- Stick-Slip-Phänomene: Reibungseigenschaften ändern sich mit der Geschwindigkeit
- Trägheitseffekte: Die Massenbeschleunigung erfordert zusätzliche Kraft/Druck
Wie berechnet man die maximal mögliche Beschleunigung in Pneumatikzylindern?
Die Kenntnis der Beschleunigungsgrenzen ist von entscheidender Bedeutung, um übermäßige Stöße, Vibrationen und den vorzeitigen Ausfall von Komponenten in pneumatischen Systemen zu verhindern.
Die maximal mögliche Beschleunigung in einem Pneumatikzylinder wird mit a = (P × A - F - Fr)/m berechnet, wobei a die Beschleunigung, P der Druck, A die Kolbenfläche, F die äußere Last, Fr der Reibungswiderstand und m die bewegte Masse ist. Diese Gleichung definiert die physikalischen Grenzen dafür, wie schnell ein pneumatischer Aktuator eine Bewegung starten oder stoppen kann.
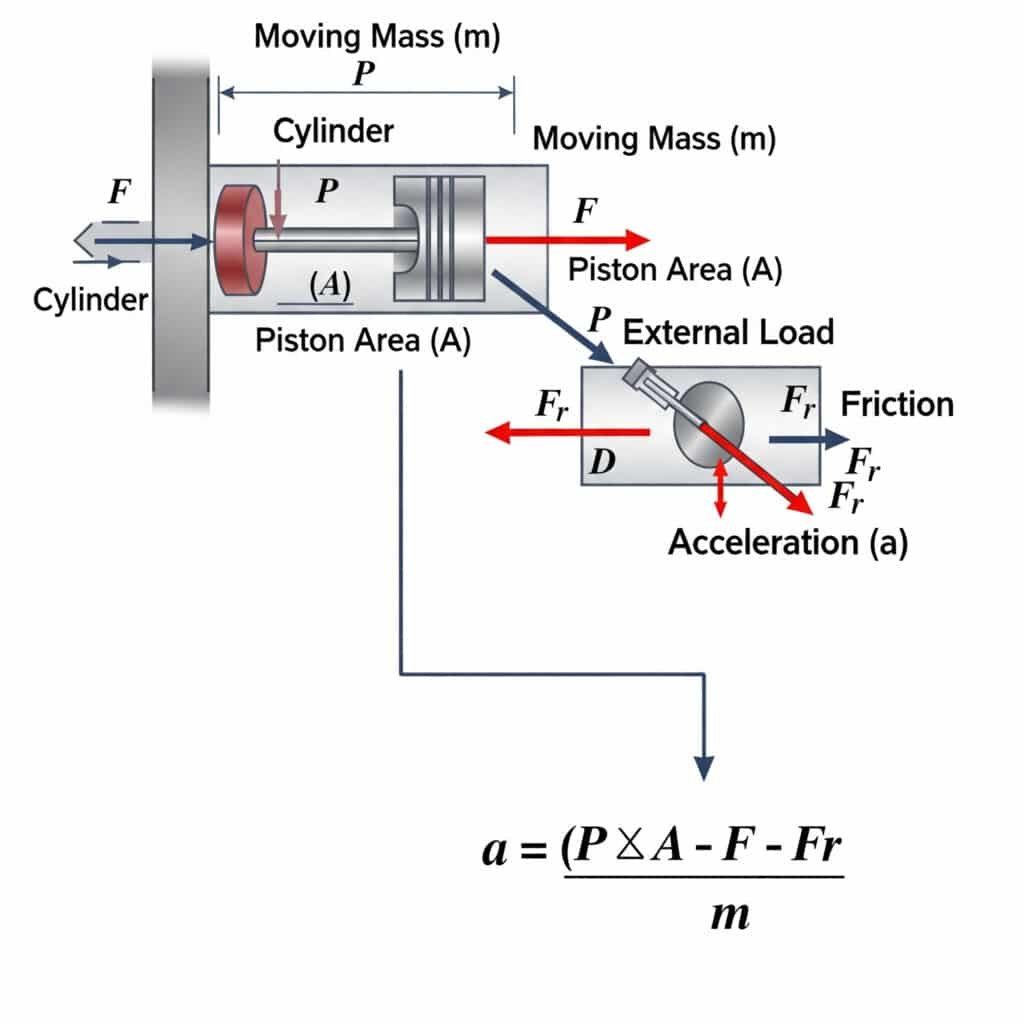
Die theoretischen Beschleunigungsgrenzen haben erhebliche praktische Auswirkungen auf den Systementwurf und die Komponentenauswahl.
Ableitung der Grenzbeschleunigungsgleichung
Die Grenzbeschleunigungsgleichung ergibt sich aus Das zweite Newtonsche Gesetz2 (F = ma):
- Die für die Beschleunigung verfügbare Nettokraft beträgt: Fnet = FDruck - FLast - FReibung
- FDruck = P × A
- Daher gilt: a = Fnet/m = (P × A - F - Fr)/m
Praktische Beschleunigungsgrenzwerte für verschiedene Zylindertypen
Verschiedene Zylinderkonstruktionen haben unterschiedliche praktische Beschleunigungsgrenzen:
| Typ des Zylinders | Typische maximale Beschleunigung | Begrenzende Faktoren |
|---|---|---|
| Standard-Stangenzylinder | 10-15 m/s² | Stangenknicken, Lagerbelastungen |
| Kolbenstangenloser Zylinder (magnetisch) | 8-12 m/s² | Magnetische Kopplungsstärke |
| Kolbenstangenloser Zylinder (mechanisch) | 15-25 m/s² | Dichtung/Lagerausführung, innere Reibung |
| Führungszylinder | 20-30 m/s² | Steifigkeit des Führungssystems, Tragfähigkeit |
| Schlagzylinder | 50-100+ m/s² | Speziell entwickelt für hohe Beschleunigung |
Berücksichtigung der Masse bei Beschleunigungsberechnungen
Bei der Berechnung der Beschleunigung ist es wichtig, alle bewegten Massen einzubeziehen:
- Montage des Kolbens: Einschließlich Kolben, Dichtungen und Verbindungselementen
- Lastmasse: Externe Last wird bewegt
- Effektive Masse der bewegten Luft: Oft vernachlässigbar, aber relevant bei Hochgeschwindigkeitsanwendungen
- Zusätzliche Masse durch Anbauteile: Halterungen, Sensoren, usw.
Ich habe einmal einem Kunden in Frankreich geholfen, der mysteriöse Ausfälle in seinem kolbenstangenlosen Zylindersystem hatte. Der Zylinder war für die angegebene Last von 15 kg richtig dimensioniert, versagte aber immer wieder nach ein paar tausend Zyklen.
Nach einer Untersuchung stellten wir fest, dass er die 12 kg Masse der Montageplatte und der Anbauteile nicht berücksichtigt hatte. Die tatsächliche bewegte Masse war fast doppelt so hoch wie die von ihm berechnete, was zu Beschleunigungskräften führte, die die Konstruktionsgrenzen des Zylinders überschritten. Nach der Umrüstung auf einen größeren Zylinder hörten die Ausfälle vollständig auf.
Methoden zur Beschleunigungskontrolle
Zur Kontrolle der Beschleunigung innerhalb sicherer Grenzen:
- Stromregelventile: Begrenzung des Durchflusses während der ersten Bewegung
- Proportionalventile: Kontrollierter Druckanstieg
- Mehrstufige Beschleunigung: Stufenweise Druckerhöhung verwenden
- Mechanische Dämpfung: Externe Stoßdämpfer hinzufügen
- Elektronische Kontrolle: Verwenden Sie servopneumatische Systeme3 mit Beschleunigungsrückmeldung
Warum ist die Dämpfungszeit wichtig und wie wird sie berechnet?
Eine ordnungsgemäße Endlagendämpfung ist für die Vermeidung von Aufprallschäden, die Verringerung von Geräuschen und die Verlängerung der Lebensdauer von Pneumatikzylindern unerlässlich. Die Kenntnis der Dämpfungszeit hilft Ingenieuren bei der Entwicklung von Systemen, die die Zykluszeit mit der Langlebigkeit der Komponenten in Einklang bringen.
Die Dämpfungszeit in Pneumatikzylindern wird anhand der Gleichung t = √(2s/a) berechnet, wobei t die Zeit, s die Dämpfungshublänge und a die Verzögerung ist. Diese Zeit gibt an, wie lange es dauert, die bewegte Masse vor dem Aufprall sicher abzubremsen, was entscheidend ist, um Schäden am Zylinder und den daran befestigten Komponenten zu verhindern.

Untersuchen wir die praktischen Aspekte der Dämpfungszeitberechnung und ihre Auswirkungen auf die Systemgestaltung.
Die Physik hinter pneumatischen Dämpfungen
Pneumatische Dämpfung funktioniert durch kontrollierte Luftkompression und gedrosselten Ausstoß:
- Wenn der Kolben in die Kissenkammer eintritt, wird der Auslassweg eingeschränkt
- Die eingeschlossene Luft wird komprimiert, wodurch ein zunehmender Gegendruck entsteht.
- Dieser Gegendruck erzeugt eine Gegenkraft, die den Kolben abbremst.
- Das Verzögerungsprofil hängt von der Konstruktion und Einstellung des Kissens ab
Berechnung der optimalen Dämpfungszeit
Die optimale Dämpfungszeit schafft ein Gleichgewicht zwischen Aufprallschutz und Zykluseffizienz:
| Parameter | Formel | Beispiel |
|---|---|---|
| Dämpfungsabstand | Basierend auf der Zylinderkonstruktion | 15mm (typisch für 40mm Bohrung) |
| Erforderliche Verzögerung | a = v²/(2s) | Für v=0,5m/s, s=15mm: a = 8,33m/s² |
| Dämpfungszeit | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Druckanstieg | P = P₀(V₀/V)^γ | Abhängig von der Geometrie der Kissenkammer |
Faktoren, die die Dämpfungsleistung beeinflussen
Mehrere Faktoren beeinflussen die tatsächliche Dämpfungsleistung:
- Dämpfende Dichtung: Beeinflusst den Luftaustritt bei der Dämpfung
- Einstellung des Nadelventils: Steuert die Abgasdrosselungsrate
- Bewegte Masse: Schwerere Lasten erfordern eine längere Dämpfungszeit
- Anfluggeschwindigkeit: Höhere Geschwindigkeiten erfordern einen längeren Polsterabstand
- Betriebsdruck: Beeinflusst die maximal verfügbare Gegenkraft
Dämpfungsarten und ihre Anwendungen
Verschiedene Dämpfungsmechanismen sind für unterschiedliche Anwendungen geeignet:
| Dämpfung Typ | Merkmale | Beste Anwendungen |
|---|---|---|
| Feste Dämpfung | Einfach, nicht einstellbar | Leichte Lasten, konstanter Betrieb |
| Einstellbare Dämpfung | Abstimmbar mit Nadelventilen | Unterschiedliche Belastungen, flexible Anwendungen |
| Selbsteinstellende Dämpfung | Passt sich an unterschiedliche Bedingungen an | Wechselnde Geschwindigkeiten und Lasten |
| Externe Stoßdämpfer | Hohe Energieabsorption | Schwere Lasten, hohe Geschwindigkeiten |
| Elektronische Dämpfung | Präzise kontrollierte Abbremsung | Servo-pneumatische Systeme |
Fallstudie: Optimierung der Dämpfung bei Anwendungen mit hoher Taktzahl
Kürzlich arbeitete ich mit Thomas, einem Konstrukteur bei einem Automobilzulieferer in Deutschland. Seine Montagelinie arbeitete mit kolbenstangenlosen Zylindern, die mit 45 Zyklen pro Minute arbeiteten, aber häufig Dichtungsausfälle und Beschädigungen der Montagehalterungen aufwiesen.
Die Analyse ergab, dass die Dämpfungszeit für die bewegte Masse zu kurz war, was zu Aufprallkräften von fast 3G an jedem Ende des Hubs führte. Durch Vergrößerung des Dämpfungshubs von 12 mm auf 20 mm und Optimierung der Nadelventileinstellungen konnte die Dämpfungszeit von 0,04 s auf 0,07 s verlängert werden.
Diese scheinbar kleine Änderung reduzierte die Aufprallkräfte um mehr als 60%, beseitigte die Beschädigung der Halterung vollständig und verlängerte die Lebensdauer der Dichtung von 3 Monaten auf über ein Jahr - und das alles unter Beibehaltung der erforderlichen Zykluszeit.
Praktisches Verfahren zur Einstellung der Dämpfung
Für optimale Dämpfungsleistung in kolbenstangenlosen Zylindern:
- Start mit vollständig geöffneten Kissenventilen (minimale Drosselung)
- Schließen Sie das Dämpfungsventil allmählich, bis eine gleichmäßige Verzögerung erreicht ist.
- Test mit minimal und maximal zu erwartenden Belastungen
- Überprüfung der Dämpfungsleistung über den gesamten Geschwindigkeitsbereich
- Achten Sie auf Aufprallgeräusche, die auf unzureichende Dämpfung hinweisen
- Messen Sie die tatsächliche Verzögerungszeit, um die Berechnungen zu bestätigen.
Schlussfolgerung
Das Verständnis der Prinzipien der Kolbenkinematik - von den Druckanforderungen für konstante Geschwindigkeiten bis hin zu Beschleunigungsgrenzen und Dämpfungszeitberechnungen - ist für die Entwicklung effizienter, zuverlässiger Pneumatiksysteme unerlässlich. Wenn Sie diese Prinzipien auf Ihre kolbenstangenlosen Zylinderanwendungen anwenden, können Sie die Leistung optimieren, den Energieverbrauch senken und die Lebensdauer der Komponenten erheblich verlängern.
FAQs zur Kolbenkinematik in pneumatischen Systemen
Welchen Druck benötige ich für eine bestimmte Zylindergeschwindigkeit?
Der erforderliche Druck hängt von der Last, der Reibung und der Zylinderfläche ab. Berechnen Sie ihn mit P = (F + Fr)/A, wobei F die externe Lastkraft, Fr der Reibungswiderstand und A die Kolbenfläche ist. Für einen typischen kolbenstangenlosen Zylinder, der eine 10 kg schwere Last horizontal bewegt, benötigen Sie etwa 1,5-2 bar für eine stabile Bewegung bei mäßigen Geschwindigkeiten.
Wie schnell kann ein Pneumatikzylinder beschleunigen?
Die maximale Beschleunigung eines Pneumatikzylinders wird mit a = (P × A - F - Fr)/m berechnet. Typische kolbenstangenlose Zylinder können je nach Konstruktion eine Beschleunigung von 10-25 m/s² erreichen. Das bedeutet, dass unter optimalen Bedingungen eine Geschwindigkeit von 0,5 m/s in etwa 20-50 Millisekunden erreicht wird.
Welche Faktoren begrenzen die Höchstgeschwindigkeit eines kolbenstangenlosen Zylinders?
Die Höchstgeschwindigkeit wird durch die Durchflusskapazität des Ventils, das Luftzufuhrvolumen, die Größe der Anschlüsse, die Dämpfungseigenschaften und die Dichtungskonstruktion begrenzt. Die meisten kolbenstangenlosen Standardzylinder sind für Höchstgeschwindigkeiten von 0,8-1,5 m/s ausgelegt, spezielle Hochgeschwindigkeitsausführungen können jedoch 2-3 m/s erreichen.
Wie berechne ich die richtige Dämpfung für meine Anwendung?
Berechnen Sie die richtige Dämpfung, indem Sie die kinetische Energie (KE = ½mv²) Ihrer bewegten Last bestimmen und sicherstellen, dass Ihr Dämpfungssystem diese Energie absorbieren kann. Die Dämpfungszeit sollte mit t = √(2s/a) berechnet werden, wobei s der Dämpfungsabstand und a die gewünschte Verzögerungsrate ist.
Was passiert, wenn mein Pneumatikzylinder zu schnell beschleunigt?
Übermäßige Beschleunigung kann zu mechanischer Beanspruchung der Montagekomponenten, vorzeitigem Verschleiß der Dichtungen, erhöhter Vibration und Geräuschentwicklung, möglicher Lastverschiebung oder Beschädigung und verringerter Systemgenauigkeit führen. Sie kann auch zu ruckartigen Bewegungen führen, die die Produktqualität bei Präzisionsanwendungen beeinträchtigen.
Wie wirkt sich die Ausrichtung der Last auf den für die Bewegung erforderlichen Druck aus?
Die Ausrichtung der Last wirkt sich erheblich auf die Druckanforderungen aus. Vertikale Lasten, die sich entgegen der Schwerkraft bewegen, benötigen zusätzlichen Druck, um die Schwerkraft zu überwinden (P = F/A + Fg/A + Fr/A). Horizontale Lasten müssen nur Reibung und Trägheit überwinden. Geneigte Lasten liegen zwischen diesen Extremen, basierend auf dem Sinus des Winkels.
-
Bietet eine grundlegende Erklärung der Kinematik, des Zweigs der Mechanik, der die Bewegung von Objekten beschreibt, ohne die Kräfte zu berücksichtigen, die die Bewegung verursachen.
elektronisches Eingangssignal, das eine erweiterte pneumatische Steuerung ermöglicht. ↩ -
Erläutert das zweite Newtonsche Gesetz (F=ma), das Grundprinzip der Physik, das die auf ein Objekt wirkende Kraft mit seiner Masse und Beschleunigung in Beziehung setzt und die Grundlage für alle dynamischen Berechnungen bildet. ↩
-
Beschreibt die Servopneumatik, eine fortschrittliche Steuerungstechnologie, die die Leistung der Pneumatik mit der Präzision der elektronischen Regelung kombiniert, um hochpräzise Positionierungs- und Bewegungsprofile zu erreichen. ↩


