
Haben Sie jemals ein Pneumatikzylinder nach dem Dauerbetrieb und sind überrascht, wie heiß es sich anfühlt? Diese Hitze ist nicht nur unangenehm, sondern steht für verschwendete Energie, verminderte Effizienz und potenzielle Zuverlässigkeitsprobleme, die Ihr Unternehmen Tausende kosten könnten.
Die Wärmeübertragung in pneumatischen Systemen erfolgt über drei Mechanismen: Wärmeleitung durch die Materialien der Komponenten, Konvektion zwischen Oberflächen und Luft und Strahlung von heißen Oberflächen. Das Verständnis und die Optimierung dieser Prinzipien können die Betriebstemperaturen um 15-30% senken, die Lebensdauer der Komponenten um bis zu 40% verlängern und die Energieeffizienz um 5-15% verbessern.
Letzten Monat beriet ich einen lebensmittelverarbeitenden Betrieb in Georgia, dessen kolbenstangenlose Zylinder alle 3 bis 4 Monate aufgrund von thermischen Problemen ausfielen. Das Wartungsteam tauschte einfach Komponenten aus, ohne die Ursache zu beheben. Durch die Anwendung geeigneter Wärmeübertragungsprinzipien konnten wir die Betriebstemperaturen um 22 °C senken und die Lebensdauer der Komponenten auf über ein Jahr verlängern. Ich möchte Ihnen zeigen, wie wir das geschafft haben - und wie Sie diese Prinzipien auch auf Ihre Systeme anwenden können.
Inhaltsübersicht
- Berechnung des Leitungskoeffizienten: Wie bewegt sich die Wärme durch Ihre Komponenten?
- Methoden zur Verbesserung der Konvektion: Welche Techniken maximieren die Wärmeübertragung zwischen Luft und Oberfläche?
- Modell des Strahlungswirkungsgrads: Wann spielt die Wärmestrahlung in pneumatischen Systemen eine Rolle?
- Schlussfolgerung
- FAQs zur Wärmeübertragung in pneumatischen Systemen
Berechnung des Leitungskoeffizienten: Wie bewegt sich die Wärme durch Ihre Komponenten?
Die Wärmeleitung ist der wichtigste Mechanismus der Wärmeübertragung in festen pneumatischen Komponenten. Das Verständnis für die Berechnung und Optimierung von Leitungskoeffizienten ist für das Management von Systemtemperaturen von entscheidender Bedeutung.
Der Wärmeleitkoeffizient kann wie folgt berechnet werden Fouriersches Gesetz1q = -k(dT/dx), wobei q der Wärmestrom (W/m²), k die Wärmeleitfähigkeit (W/m-K) und dT/dx das Temperaturgefälle ist. Bei pneumatischen Komponenten hängt die effektive Wärmeleitung von der Materialauswahl, der Qualität der Schnittstellen und geometrischen Faktoren ab, die die Länge des Wärmewegs und die Querschnittsfläche beeinflussen.
Ich erinnere mich an die Fehlersuche in einer Fertigungslinie in Tennessee, wo die kolbenstangenlosen Zylinderlager vorzeitig ausfielen. Das Wartungsteam hatte mehrere Schmiermittel ohne Erfolg ausprobiert. Als wir die Leitungswege analysierten, entdeckten wir einen thermischen Engpass an der Schnittstelle zwischen Lager und Gehäuse. Durch die Verbesserung der Oberflächenbeschaffenheit und das Auftragen einer wärmeleitenden Verbindung konnten wir den effektiven Leitungskoeffizienten um 340% erhöhen und die Ausfälle vollständig beseitigen.
Grundlegende Gleichungen zur Wärmeleitung
Im Folgenden werden die wichtigsten Gleichungen zur Berechnung der Leitfähigkeit von pneumatischen Komponenten erläutert:
Fouriersches Gesetz der Wärmeleitung
Die Grundgleichung für die Wärmeleitung lautet:
q = -k(dT/dx)
Wo:
- q = Wärmestrom (W/m²)
- k = Wärmeleitfähigkeit (W/m-K)
- dT/dx = Temperaturgefälle (K/m)
Für einen einfachen eindimensionalen Fall mit konstantem Querschnitt:
Q = kA(T₁-T₂)/L
Wo:
- Q = Wärmeübertragungsrate (W)
- A = Querschnittsfläche (m²)
- T₁, T₂ = Temperaturen an jedem Ende (K)
- L = Länge des Wärmeweges (m)
Konzept des thermischen Widerstands
Bei komplexen Geometrien ist der Ansatz des Wärmewiderstands oft praktischer:
R = L/(kA)
Wo:
- R = Wärmewiderstand (K/W)
Für Systeme mit mehreren in Reihe geschalteten Komponenten:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
Und die Wärmeübertragungsrate wird:
Q = ΔT/Rtotal
Vergleich der Wärmeleitfähigkeit von Materialien
| Material | Wärmeleitfähigkeit (W/m-K) | Relative Leitfähigkeit | Gemeinsame Anwendungen |
|---|---|---|---|
| Aluminium | 205-250 | Hoch | Zylinder, Wärmesenken |
| Stahl | 36-54 | Mittel | Strukturelle Komponenten |
| Rostfreier Stahl | 14-16 | Niedrig bis mittel | Korrosive Umgebungen |
| Bronze | 26-50 | Mittel | Lager, Buchsen |
| PTFE | 0.25 | Sehr niedrig | Dichtungen, Lager |
| Nitrilkautschuk | 0.13 | Sehr niedrig | O-Ringe, Dichtungen |
| Luft (still) | 0.026 | Äußerst gering | Lückenfüller |
| Wärmeleitpaste | 3-8 | Niedrig | Material der Schnittstelle |
Kontaktwiderstand in pneumatischen Baugruppen
An den Schnittstellen zwischen den Bauteilen beeinflusst der Kontaktwiderstand die Wärmeübertragung erheblich:
RKontakt = 1/(hc × A)
Wo:
- hc = Kontaktkoeffizient (W/m²-K)
- A = Kontaktfläche (m²)
Zu den Faktoren, die den Kontaktwiderstand beeinflussen, gehören:
- Oberflächenrauhigkeit: Rauere Oberflächen haben eine geringere tatsächliche Kontaktfläche
- Kontakt Druck: Höherer Druck vergrößert die effektive Kontaktfläche
- Schnittstelle Materialien: Wärmeleitpasten füllen Luftspalten
- Sauberkeit der Oberfläche: Verunreinigungen können die Resistenz erhöhen
Fallstudie: Thermische Optimierung von kolbenstangenlosen Zylindern
Für einen magnetischen kolbenstangenlosen Zylinder, der thermische Probleme aufweist:
| Komponente | Originelles Design | Optimiertes Design | Verbesserung |
|---|---|---|---|
| Zylindergehäuse | Eloxiertes Aluminium | Gleiches Material, verbesserte Verarbeitung | 15% bessere Leitfähigkeit |
| Lager Schnittstelle | Metall-auf-Metall-Kontakt | Zusätzliche Wärmeleitpaste | 340% bessere Leitfähigkeit |
| Montagebügel | Lackierter Stahl | Blankes Aluminium | 280% bessere Leitfähigkeit |
| Thermischer Gesamtwiderstand | 2,8 K/W | 0,7 K/W | 75% Ermäßigung |
| Betriebstemperatur | 78°C | 56°C | 22°C Reduzierung |
| Bauteil Lebensdauer | 4 Monate | >12 Monate | 3× Verbesserung |
Praktische Techniken zur Optimierung der Leitfähigkeit
Basierend auf meiner Erfahrung mit Hunderten von pneumatischen Systemen, sind hier die effektivsten Ansätze zur Verbesserung der Leitfähigkeit:
Optimierung der Schnittstelle
- Oberflächenveredelung: Verbesserung der Glätte der Gegenlauffläche auf Ra 0,4-0,8 μm
- Thermische Grenzflächenmaterialien2: Geeignete Verbindungen auftragen (3-8 W/m-K)
- Anzugsmoment der Befestigungsmittel: Richtiges Anziehen für optimalen Anpressdruck sicherstellen
- Sauberkeit: Entfernen Sie vor der Montage alle Öle und Verunreinigungen
Strategien für die Materialauswahl
- Kritische Wärmepfade: Verwenden Sie Materialien mit hoher Leitfähigkeit (Aluminium, Kupfer)
- Thermische Pausen: Bewusste Verwendung von Materialien mit geringer Leitfähigkeit zur Isolierung von Wärme
- Komposit-Ansätze: Kombinieren Sie Materialien für optimale Leistung/Kosten
- Anisotrope Materialien: Nutzen Sie die gerichtete Leitfähigkeit, wo es angebracht ist
Geometrische Optimierung
- Länge der Wärmestrecke: Minimierung des Abstands zwischen Wärmequellen und -senken
- Querschnittliche Fläche: Maximierung der Fläche senkrecht zum Wärmestrom
- Thermische Engpässe: Identifizierung und Beseitigung von Engpässen im Wärmeweg
- Redundante Pfade: Mehrere parallele Leitungswege schaffen
Methoden zur Verbesserung der Konvektion: Welche Techniken maximieren die Wärmeübertragung zwischen Luft und Oberfläche?
Konvektion ist oft der begrenzende Faktor bei der Kühlung pneumatischer Systeme. Die Verbesserung der konvektiven Wärmeübertragung kann das Wärmemanagement und die Systemleistung drastisch verbessern.
Die konvektive Wärmeübertragung erfolgt Newtons Gesetz der Abkühlung3: Q = hA(Ts-T∞), wobei h der Konvektionskoeffizient (W/m²-K), A die Oberfläche und (Ts-T∞) der Temperaturunterschied zwischen der Oberfläche und der Flüssigkeit ist. Zu den Verbesserungsmethoden gehören die Vergrößerung der Oberfläche durch Rippen, die Verbesserung der Flüssigkeitsgeschwindigkeit durch gerichtete Luftströmung und die Optimierung der Oberflächeneigenschaften zur Förderung turbulenter Grenzschichten.
Bei einem Energieeffizienz-Audit in einer Verpackungsanlage in Arizona stieß ich auf ein pneumatisches System, das bei einer Umgebungstemperatur von 43 °C betrieben wurde. Die kolbenstangenlosen Zylinder überhitzten, obwohl sie alle Wartungsanforderungen erfüllten. Durch gezielte Konvektionsverbesserung - kleine Aluminiumrippen und ein stromsparender Lüfter - konnten wir den Konvektionskoeffizienten um 450% erhöhen. Dadurch konnten wir die Betriebstemperaturen von gefährlichen Werten auf einen Wert innerhalb der Spezifikationen senken, ohne dass größere Systemänderungen erforderlich waren.
Grundlagen der Konvektionswärmeübertragung
Die Grundgleichung für den konvektiven Wärmeübergang lautet:
Q = hA(Ts-T∞)
Wo:
- Q = Wärmeübertragungsrate (W)
- h = Konvektionskoeffizient (W/m²-K)
- A = Oberfläche (m²)
- Ts = Oberflächentemperatur (K)
- T∞ = Temperatur der Flüssigkeit (Luft) (K)
Der Konvektionskoeffizient h hängt von mehreren Faktoren ab:
- Flüssigkeitseigenschaften (Dichte, Viskosität, Wärmeleitfähigkeit)
- Strömungseigenschaften (Geschwindigkeit, Turbulenz)
- Oberflächengeometrie und Ausrichtung
- Strömungsregime (natürliche vs. erzwungene Konvektion)
Natürliche vs. erzwungene Konvektion
| Parameter | Natürliche Konvektion | Zwangskonvektion | Auswirkungen |
|---|---|---|---|
| Typischer h-Wert | 5-25 W/m²-K | 25-250 W/m²-K | Erzwungene Konvektion kann 10x effektiver sein |
| Treibende Kraft | Auftrieb (Temperaturunterschied) | Externer Druck (Ventilatoren, Gebläse) | Erzwungene Konvektion ist weniger abhängig von der Temperatur |
| Strömungsmuster | Vertikale Strömung entlang von Oberflächen | Richtungsabhängig nach dem Triebmechanismus | Der erzwungene Durchfluss kann für bestimmte Komponenten optimiert werden |
| Verlässlichkeit | Passiv, immer präsent | Erfordert Strom und Wartung | Natürliche Konvektion sorgt für Basiskühlung |
| Platzbedarf | Erfordert Freiraum für die Luftzirkulation | Benötigt Platz für Luftumwälzer und Leitungen | Forcierte Systeme erfordern mehr Planung |
Techniken zur Verbesserung der Konvektion
Vergrößerung der Oberfläche
Vergrößerung der effektiven Oberfläche durch:
Flossen und erweiterte Oberflächen
- Stift-Lamellen: Omnidirektionaler Luftstrom, 150-300% Flächenvergrößerung
- Plattenlamellen: Gerichteter Luftstrom, 200-500% Flächenvergrößerung
- Gewellte Oberflächen: Mäßige Verstärkung, 50-150% FlächenvergrößerungOberfläche aufrauen
- Mikrotexturierung: 5-15% Erhöhung der effektiven Fläche
- Vertiefte Oberflächen: 10-30% Erhöhung plus Grenzschichteffekte
- Gerillte Muster: 15-40% Erhöhung mit richtungsweisenden Vorteilen
Flussmanipulation
Verbesserung der Luftstromeigenschaften durch:
Systeme mit Zwangsbelüftung
- Ventilatoren: gerichteter Luftstrom, 200-600% h Verbesserung
- Gebläse: Hochdruckstrom, 300-800% h Verbesserung
- Druckluftdüsen: Gezielte Kühlung, 400-1000% lokale h VerbesserungOptimierung der Fließwege
- Luftleitbleche: Leiten Sie Luft zu kritischen Komponenten
- Venturi-Effekte: Beschleunigung der Luft über bestimmte Oberflächen
- Wirbelgeneratoren: Erzeugen von Turbulenzen zur Unterbrechung der Grenzschicht
Änderungen der Oberfläche
Veränderung der Oberflächeneigenschaften zur Verbesserung der Konvektion:
Emissivität Behandlungen
- Schwarzes Oxid: Erhöht den Emissionsgrad auf 0,7-0,9
- Eloxieren: Kontrollierter Emissionsgrad von 0,4-0,9
- Anstriche und Beschichtungen: Anpassbarer Emissionsgrad bis zu 0,98Kontrolle der Benetzbarkeit
- Hydrophile Beschichtungen: Verbessern die Flüssigkeitskühlung
- Hydrophobe Oberflächen: Verhinderung von Kondensationsproblemen
- Gemusterte Benetzbarkeit: Gerichteter Kondensatfluss
Praktisches Umsetzungsbeispiel
Für einen kolbenstangenlosen Pneumatikzylinder, der in einer Hochtemperaturumgebung betrieben wird:
| Enhancement-Methode | Umsetzung | h Verbesserung | Senkung der Temperatur |
|---|---|---|---|
| Stiftflossen (6mm) | Aufsteckbare Aluminium-Lamellen, 10 mm Abstand | 180% | 12°C |
| Gerichteter Luftstrom | 80mm, 2W DC-Lüfter bei 1,5 m/s | 320% | 18°C |
| Oberflächenbehandlung | Schwarz eloxiert | 40% | 3°C |
| Kombinierter Ansatz | Alle Methoden integriert | 450% | 24°C |
Nusselt-Zahl-Korrelation für Konstruktionsberechnungen
Für technische Berechnungen ist die Nusselt-Zahl4 (Nu) bietet einen dimensionslosen Ansatz für die Konvektion:
Nu = hL/k
Wo:
- L = charakteristische Länge
- k = Wärmeleitfähigkeit der Flüssigkeit
Für erzwungene Konvektion über eine flache Platte:
Nu = 0,664Re^(1/2)Pr^(1/3) (laminare Strömung)
Nu = 0,037Re^(4/5)Pr^(1/3) (turbulente Strömung)
Wo:
- Re = Reynoldszahl (Geschwindigkeit × Länge × Dichte / Viskosität)
- Pr = Prandtl-Zahl (spezifische Wärme × Viskosität / Wärmeleitfähigkeit)
Diese Korrelationen ermöglichen es den Ingenieuren, Konvektionskoeffizienten für verschiedene Konfigurationen vorherzusagen und die Kühlstrategien entsprechend zu optimieren.
Modell des Strahlungswirkungsgrads: Wann spielt die Wärmestrahlung in pneumatischen Systemen eine Rolle?
Strahlung wird beim Wärmemanagement von Pneumatiksystemen oft übersehen, obwohl sie bei vielen Anwendungen 15-30% der gesamten Wärmeübertragung ausmachen kann. Für ein umfassendes Wärmemanagement ist es entscheidend zu verstehen, wann und wie die Strahlungswärmeübertragung optimiert werden kann.
Die Strahlungswärmeübertragung folgt der Stefan-Boltzmann-Gesetz5: Q = εσA(T₁⁴-T₂⁴), wobei ε der Emissionsgrad der Oberfläche, σ die Stefan-Boltzmann-Konstante, A die Oberfläche und T₁ und T₂ die absoluten Temperaturen der emittierenden Oberfläche und der Umgebung sind. Die Strahlungseffizienz in pneumatischen Systemen hängt in erster Linie vom Emissionsgrad der Oberfläche, der Temperaturdifferenz und den Sichtfaktoren zwischen den Komponenten und ihrer Umgebung ab.
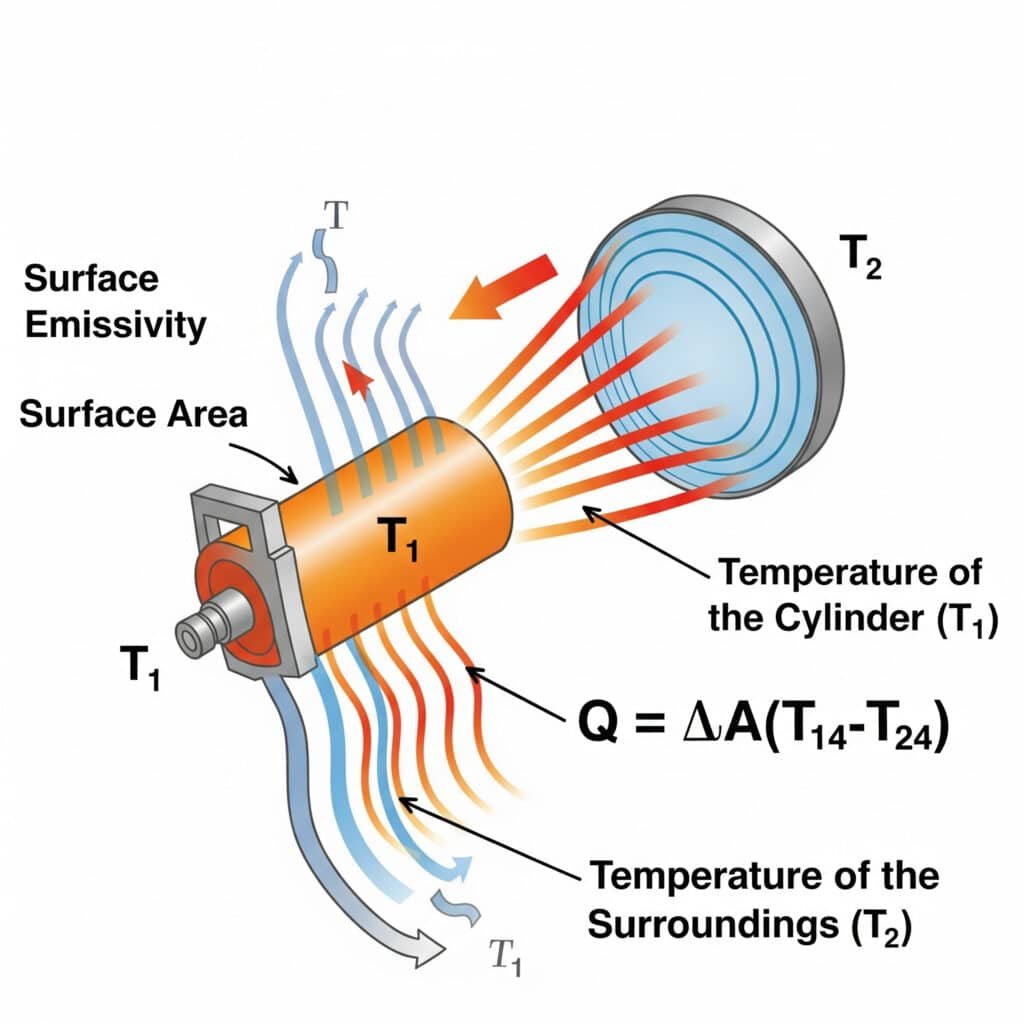
Vor kurzem habe ich einem Hersteller von Halbleiterausrüstung in Oregon geholfen, Überhitzungsprobleme mit seinen kolbenstangenlosen Präzisionszylindern zu lösen. Die Ingenieure des Unternehmens hatten sich ausschließlich auf Wärmeleitung und Konvektion konzentriert, aber die Strahlung übersehen. Durch Aufbringen einer Beschichtung mit hohem Emissionsgrad (Erhöhung von ε von 0,11 auf 0,92) konnten wir die Strahlungswärmeübertragung um über 700% verbessern. Diese einfache, passive Lösung senkte die Betriebstemperaturen um 9 °C ohne bewegliche Teile oder Energieverbrauch - eine wichtige Anforderung in der Reinraumumgebung.
Grundlagen der Strahlungswärmeübertragung
Die Grundgleichung für die Strahlungswärmeübertragung lautet:
Q = εσA(T₁⁴-T₂⁴)
Wo:
- Q = Wärmeübertragungsrate (W)
- ε = Emissionsgrad (dimensionslos, 0-1)
- σ = Stefan-Boltzmann-Konstante (5,67 × 10-⁸ W/m²-K⁴)
- A = Oberfläche (m²)
- T₁ = absolute Oberflächentemperatur (K)
- T₂ = absolute Temperatur der Umgebung (K)
Oberflächenemissionswerte für gängige pneumatische Materialien
| Material/Oberfläche | Emissionsgrad (ε) | Strahlungseffizienz | Erweiterungspotenzial |
|---|---|---|---|
| Poliertes Aluminium | 0.04-0.06 | Sehr Schlecht | >1500% Verbesserung möglich |
| Eloxiertes Aluminium | 0.7-0.9 | Ausgezeichnet | Bereits optimiert |
| Rostfreier Stahl (poliert) | 0.07-0.14 | Schlecht | >600% Verbesserung möglich |
| Rostfreier Stahl (oxidiert) | 0.6-0.85 | Gut | Mäßige Verbesserung möglich |
| Stahl (poliert) | 0.07-0.10 | Schlecht | >900% Verbesserung möglich |
| Stahl (oxidiert) | 0.7-0.9 | Ausgezeichnet | Bereits optimiert |
| Lackierte Oberflächen | 0.8-0.98 | Ausgezeichnet | Bereits optimiert |
| PTFE (weiß) | 0.8-0.9 | Ausgezeichnet | Bereits optimiert |
| Nitrilkautschuk | 0.86-0.94 | Ausgezeichnet | Bereits optimiert |
Ansicht Faktor Überlegungen
Der Strahlungsaustausch hängt nicht nur vom Emissionsgrad, sondern auch von den geometrischen Beziehungen zwischen den Oberflächen ab:
F₁₂ = Anteil der von Oberfläche 1 ausgehenden Strahlung, die auf Oberfläche 2 trifft
Für komplexe Geometrien können die Ansichtsfaktoren mit Hilfe berechnet werden:
- Analytische Lösungen für einfache Geometrien
- Ansicht Faktor Algebra für die Kombination bekannter Lösungen
- Numerische Methoden für komplexe Arrangements
- Empirische Näherungen für die praktische Technik
Temperaturabhängigkeit der Strahlung
Aufgrund des Temperaturverhältnisses der vierten Potenz ist die Strahlung bei höheren Temperaturen besonders wirksam:
| Oberflächentemperatur | Prozentsatz der Wärmeübertragung durch Strahlung* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Annahme natürlicher Konvektionsbedingungen, ε = 0,8, 25°C Umgebungstemperatur
Strategien zur Verbesserung der Strahlungseffizienz
Basierend auf meiner Erfahrung mit industriellen pneumatischen Systemen, sind hier die effektivsten Ansätze zur Verbesserung der Strahlungswärmeübertragung:
Änderung des Emissionsgrads der Oberfläche
Hoch-emissionsfähige Beschichtungen
- Schwarzes Eloxieren für Aluminium (ε ≈ 0,8-0,9)
- Schwarzes Oxid für Stahl (ε ≈ 0,7-0,8)
- Spezialkeramische Beschichtungen (ε ≈ 0,9-0,98)Oberflächenstrukturierung
- Mikroaufrauung erhöht die effektive Emissivität
- Poröse Oberflächen verbessern die Strahlungseigenschaften
- Kombinierte Emissionsgrad-/Konvektionsverbesserungen
Optimierung der Umwelt
Umgebungs-Temperaturmanagement
- Abschirmung von heißen Geräten/Prozessen
- Kühle Wände/Decken für besseren Strahlungsaustausch
- Reflektierende Barrieren, um die Strahlung auf kühlere Oberflächen zu lenkenAnsicht Faktorverbesserung
- Ausrichtung, um die Exposition gegenüber kühlen Oberflächen zu maximieren
- Beseitigung von blockierenden Gegenständen
- Reflektoren zur Verbesserung des Strahlungsaustauschs mit kühleren Gebieten
Fallstudie: Strahlungsverbesserung in der Präzisionspneumatik
Für einen hochpräzisen kolbenstangenlosen Zylinder in einer Reinraumumgebung:
| Parameter | Originelles Design | Strahlungsoptimiertes Design | Verbesserung |
|---|---|---|---|
| Oberfläche Material | Poliertes Aluminium (ε ≈ 0,06) | Keramisch beschichtetes Aluminium (ε ≈ 0,94) | 1467% Erhöhung der Emissivität |
| Strahlungswärmeübertragung | 2.1W | 32.7W | 1457% Erhöhung der Strahlung |
| Betriebstemperatur | 68°C | 59°C | 9°C Reduzierung |
| Bauteil Lebensdauer | 8 Monate | >24 Monate | 3× Verbesserung |
| Durchführung Kosten | – | $175 pro Zylinder | 4,2 Monate Amortisation |
Strahlung vs. andere Wärmeübertragungsmodi
Für ein effizientes Wärmemanagement ist es entscheidend zu wissen, wann die Strahlung dominiert:
| Zustand | Leitungsdominanz | Dominanz der Konvektion | Strahlungsdominanz |
|---|---|---|---|
| Temperaturbereich | Niedrig bis Hoch | Niedrig bis mittel | Mittel bis Hoch |
| Materialeigenschaften | Hohe k-Materialien | Niedriges k, große Oberfläche | Hohe ε-Oberflächen |
| Umweltfaktoren | Guter thermischer Kontakt | Luftbewegung, Ventilatoren | Große Temperaturunterschiede |
| Platzbeschränkungen | Straffe Verpackung | Offener Luftstrom | Blick auf die kühlere Umgebung |
| Beste Anwendungen | Schnittstellen der Komponenten | Allgemeine Kühlung | Heiße Oberflächen, Vakuum, ruhige Luft |
Schlussfolgerung
Die Beherrschung der Prinzipien der Wärmeübertragung - Berechnung des Leitungskoeffizienten, Methoden zur Verbesserung der Konvektion und Modellierung der Strahlungseffizienz - bildet die Grundlage für ein effektives Wärmemanagement in pneumatischen Systemen. Durch die Anwendung dieser Prinzipien können Sie die Betriebstemperaturen senken, die Lebensdauer der Komponenten verlängern und die Energieeffizienz verbessern und gleichzeitig einen zuverlässigen Betrieb auch in schwierigen Umgebungen gewährleisten.
FAQs zur Wärmeübertragung in pneumatischen Systemen
Wie hoch ist der typische Temperaturanstieg in Pneumatikzylindern während des Betriebs?
Bei Pneumatikzylindern kommt es im Dauerbetrieb in der Regel zu einem Temperaturanstieg von 20-40 °C über die Umgebungstemperatur. Dieser Anstieg resultiert aus der Reibung zwischen Dichtungen und Zylinderwänden, der Kompressionserwärmung der Luft und der Umwandlung mechanischer Arbeit in Wärme. Bei kolbenstangenlosen Zylindern ist der Temperaturanstieg oft höher (30-50 °C), da die Dichtungssysteme komplexer sind und die Wärmeerzeugung sich auf die Lager/Dichtungen konzentriert.
Wie wirkt sich der Betriebsdruck auf die Wärmeentwicklung in pneumatischen Systemen aus?
Der Betriebsdruck hat einen erheblichen Einfluss auf die Wärmeerzeugung, wobei höhere Drücke durch mehrere Mechanismen mehr Wärme erzeugen. Jeder Anstieg des Betriebsdrucks um 1 bar erhöht die Wärmeentwicklung typischerweise um 8-12% aufgrund größerer Reibungskräfte zwischen Dichtungen und Oberflächen, höherer Kompressionserwärmung und erhöhter leckagebedingter Verluste. Diese Beziehung ist innerhalb normaler Betriebsbereiche (3-10 bar) ungefähr linear.
Was ist der optimale Kühlungsansatz für pneumatische Komponenten in verschiedenen Umgebungen?
Der optimale Kühlungsansatz variiert je nach Umgebung: In sauberen Umgebungen mit moderaten Temperaturen (15-30 °C) ist eine natürliche Konvektion mit angemessenem Abstand zwischen den Komponenten oft ausreichend. In Umgebungen mit hohen Temperaturen (30-50 °C) ist eine erzwungene Konvektion mit Lüftern oder Druckluft erforderlich. In extrem heißen Umgebungen (>50°C) oder bei eingeschränktem Luftstrom können aktive Kühlmethoden wie thermoelektrische Kühler oder Flüssigkeitskühlung erforderlich sein. In allen Fällen sorgt die Maximierung der Strahlung durch Oberflächen mit hohem Emissionsvermögen für zusätzliche passive Kühlung.
Wie berechnet man den Gesamtwärmeübergang einer pneumatischen Komponente?
Berechnen Sie die gesamte Wärmeübertragung, indem Sie die Beiträge der einzelnen Mechanismen addieren: QGesamt = QKonduktion + QKonvektion + QStrahlung. Für die Wärmeleitung verwenden Sie Q = kA(T₁-T₂)/L für jeden Wärmepfad. Für Konvektion ist Q = hA(Ts-T∞) mit entsprechenden Konvektionskoeffizienten zu verwenden. Für Strahlung ist Q = εσA(T₁⁴-T₂⁴) zu verwenden. Bei den meisten industriellen pneumatischen Anwendungen, die bei 30-80°C betrieben werden, beträgt die ungefähre Verteilung 20-40% Leitung, 40-70% Konvektion und 10-30% Strahlung.
Welcher Zusammenhang besteht zwischen der Temperatur und der Lebensdauer von Pneumatikkomponenten?
Die Lebensdauer von Bauteilen nimmt mit steigender Temperatur exponentiell ab und folgt dabei einer modifizierten Arrhenius-Beziehung. Als Faustregel gilt, dass jede Erhöhung der Betriebstemperatur um 10 °C die Lebensdauer von Dichtungen und Bauteilen um 40-50% verringert. Das bedeutet, dass ein Bauteil, das bei 70 °C betrieben wird, möglicherweise nur ein Drittel so lange hält wie das gleiche Bauteil bei 50 °C. Diese Beziehung ist besonders kritisch für Polymerkomponenten wie Dichtungen, Lager und Dichtungen, die oft das Wartungsintervall für pneumatische Systeme bestimmen.
-
Bietet eine grundlegende Erklärung des Fourier'schen Gesetzes, des fundamentalen Prinzips, das beschreibt, wie Wärme durch feste Materialien geleitet wird, basierend auf deren Wärmeleitfähigkeit und Temperaturgradient. ↩
-
Erklärt die Funktion und die Arten von Wärmeschnittstellenmaterialien (TIMs), die zum Füllen mikroskopisch kleiner Luftspalten zwischen Komponenten verwendet werden, um die Wärmeleitung zu verbessern und den Wärmewiderstand zu verringern. ↩
-
Erläutert die Prinzipien des Newton'schen Kühlungsgesetzes, das bestimmt, wie Objekte durch die Übertragung von Wärme an die umgebende Flüssigkeit mittels Konvektion abkühlen, ein Schlüsselfaktor bei der Konstruktion von Kühlsystemen. ↩
-
Bietet einen detaillierten Einblick in die Nusselt-Zahl, eine kritische dimensionslose Größe in der Strömungsdynamik und Wärmeübertragung, die das Verhältnis zwischen konvektiver und konduktiver Wärmeübertragung an einer Grenzfläche darstellt. ↩
-
Beschreibt das Stefan-Boltzmann-Gesetz, das grundlegende physikalische Prinzip, das die Gesamtenergie, die von einem schwarzen Körper abgestrahlt wird, quantifiziert und das für die Berechnung des Wärmeverlusts von heißen Oberflächen unerlässlich ist. ↩


