Der Alptraum eines jeden Wartungstechnikers ist der unerwartete Ausfall einer Maschine. Wenn Maschinen in ihrer Eigenfrequenz schwingen, können innerhalb von Minuten katastrophale Schäden entstehen. Ich habe erlebt, wie dieses Problem Unternehmen Tausende von Ausfallzeiten gekostet hat.
Schwingungsresonanz1 tritt auf, wenn eine äußere Kraft mit der Eigenfrequenz eines Systems übereinstimmt und verstärkte Schwingungen verursacht, die die Ausrüstung beschädigen können. Das Verständnis und die Kontrolle dieses Phänomens sind wichtig, um Ausfälle zu verhindern und die Lebensdauer von Maschinen zu verlängern.
Lassen Sie mich eine kurze Geschichte erzählen. Letztes Jahr rief mich ein Kunde aus Deutschland in Panik an. Seine Produktionslinie war zum Stillstand gekommen, weil ein kolbenstangenloser Zylinder hat heftig vibriert. Das Problem? Resonanz. Am Ende dieses Artikels werden Sie wissen, wie Sie ähnliche Probleme in Ihren Systemen erkennen und verhindern können.
Inhaltsübersicht
- Eigenfrequenz-Formel: Wie können Sie die gefährdeten Punkte Ihres Systems berechnen?
- Masse-Feder-Modell: Warum ist dieser vereinfachte Ansatz so wertvoll?
- Optimierung des Dämpfungsverhältnisses: Welche Experimente führen zu den besten Ergebnissen?
- Schlussfolgerung
- FAQs zur Schwingungsresonanz
Eigenfrequenz-Formel: Wie können Sie die gefährdeten Punkte Ihres Systems berechnen?
Die Kenntnis der Eigenfrequenz Ihres Geräts ist der erste Schritt zur Vermeidung von Resonanzproblemen. Dieser kritische Wert bestimmt, wann Ihr System am anfälligsten für Schwingungsprobleme ist.
Die Eigenfrequenz2 (fn) eines Systems lässt sich nach folgender Formel berechnen: fn = (1/2π) × √(k/m), wobei k der Steifigkeitskoeffizient und m die Masse ist. Diese Berechnung gibt Aufschluss über die Frequenz, bei der Ihr System in Resonanz gerät, wenn es durch entsprechende äußere Kräfte angeregt wird.
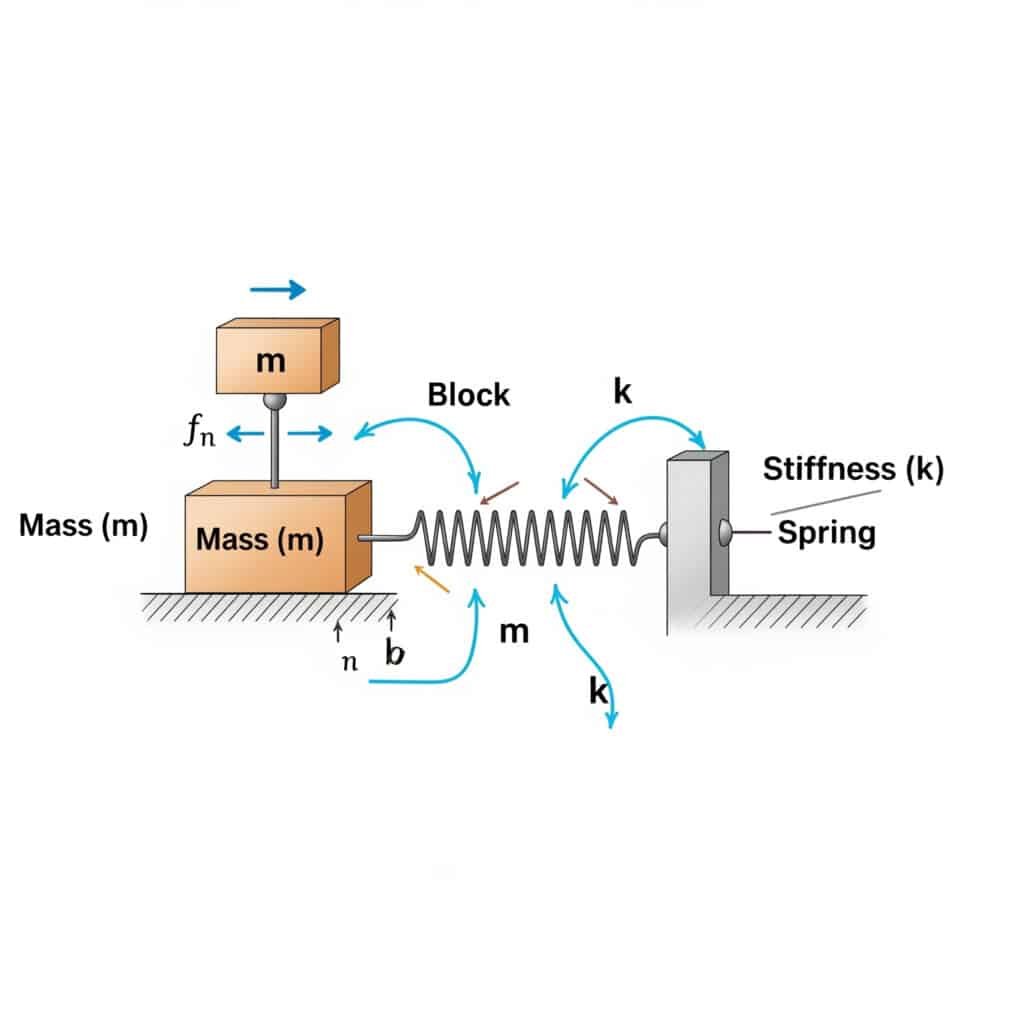
Bei einem Besuch in einem Schweizer Produktionsbetrieb stellte ich fest, dass die kolbenstangenlosen Pneumatikzylinder vorzeitig ausfielen. Das Wartungsteam hatte die Eigenfrequenz der Anlage nicht berechnet. Nach Anwendung dieser Formel stellten wir fest, dass ihre Betriebsgeschwindigkeit gefährlich nahe an der Eigenfrequenz des Systems lag.
Praktische Anwendungen von Eigenfrequenzberechnungen
Die Formel für die Eigenfrequenz ist nicht nur theoretisch, sondern findet auch direkte Anwendung in verschiedenen industriellen Bereichen:
- Auswahl der Ausrüstung: Auswahl von Komponenten mit Eigenfrequenzen, die weit von Ihren Betriebsbedingungen entfernt sind
- Vorbeugende Wartung: Planung von Inspektionen auf der Grundlage von Vibrationsrisikoprofilen
- Fehlersuche: Ermittlung der Ursache für unerwartete Vibrationen
Gemeinsame Eigenfrequenzwerte für industrielle Komponenten
| Komponente | Typischer Eigenfrequenzbereich (Hz) |
|---|---|
| Kolbenstangenlose Zylinder | 10-50 Hz |
| Montagebügel | 20-100 Hz |
| Unterstützende Strukturen | 5-30 Hz |
| Steuerventile | 40-200 Hz |
Kritische Faktoren, die die Eigenfrequenz beeinflussen
Die Berechnung der Eigenfrequenz scheint einfach zu sein, aber mehrere Faktoren können die Anwendung in der Praxis erschweren:
- Ungleichmäßige Massenverteilung: Die meisten industriellen Komponenten haben keine perfekt verteilte Masse
- Variable Steifigkeit: Komponenten können in verschiedenen Richtungen unterschiedliche Steifigkeit aufweisen
- Anschlussstellen: Die Art der Montage von Bauteilen hat erheblichen Einfluss auf deren Schwingungseigenschaften
- Auswirkungen der Temperatur: Sowohl die Masse als auch die Steifigkeitseigenschaften können sich mit der Temperatur verändern.
Masse-Feder-Modell: Warum ist dieser vereinfachte Ansatz so wertvoll?
Das Masse-Feder-Modell bietet einen intuitiven Rahmen für das Verständnis komplexer Schwingungssysteme. Es reduziert komplizierte Maschinen auf grundlegende Elemente, die Ingenieure leicht analysieren können.
Die Masse-Feder-Modell3 vereinfacht die Schwingungsanalyse, indem es mechanische Systeme als diskrete, durch Federn verbundene Massen darstellt. Dieser Ansatz ermöglicht es Ingenieuren, das Systemverhalten vorherzusagen, potenzielle Resonanzprobleme zu erkennen und effektive Lösungen ohne komplexe Mathematik zu entwickeln.
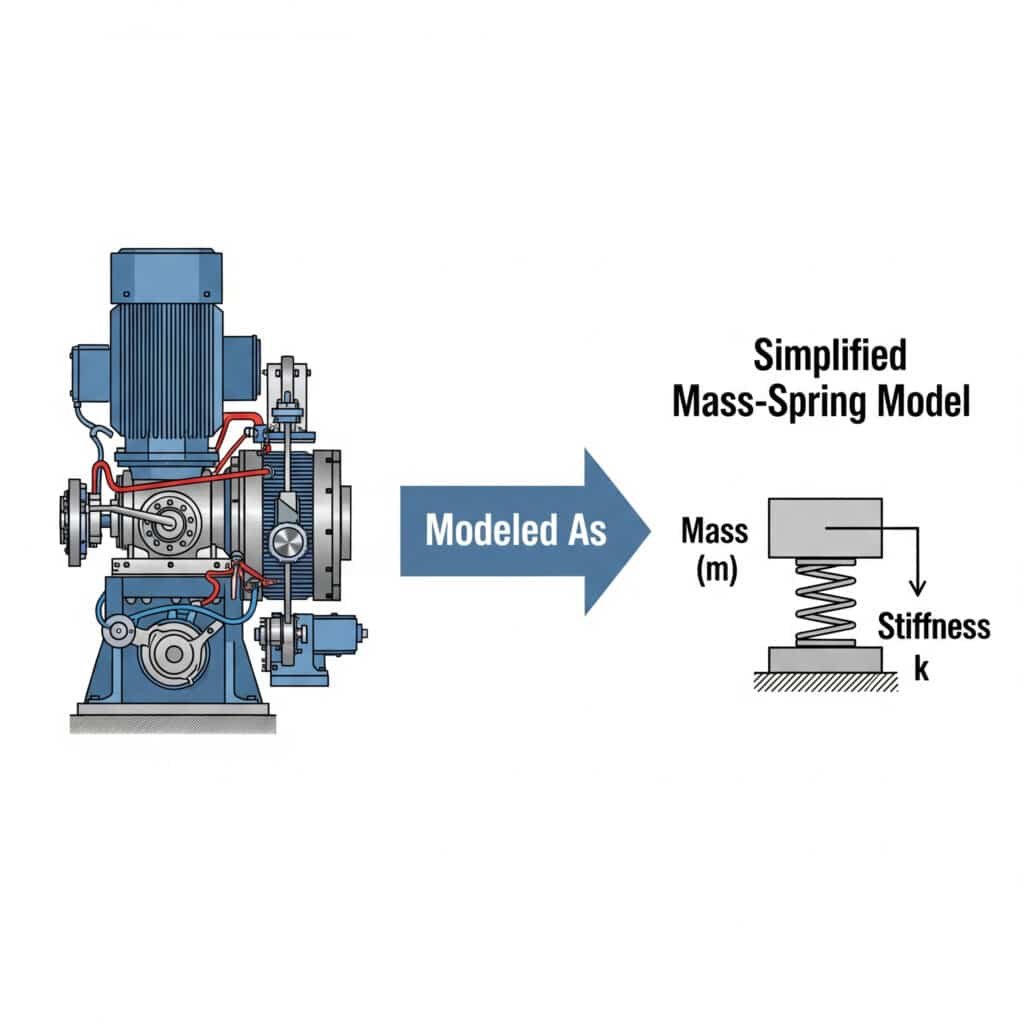
Ich erinnere mich an eine Zusammenarbeit mit einem Hersteller von Kraftfahrzeugteilen in Michigan, der nicht verstehen konnte, warum seine geführten kolbenstangenlosen Zylinder versagten. Indem wir das System als einfache Masse-Feder-Anordnung modellierten, konnten wir feststellen, dass die Montagehalterungen als unbeabsichtigte Federn wirkten und einen Resonanzzustand erzeugten.
Umwandlung realer Systeme in Masse-Feder-Modelle
Um diesen Ansatz auf Ihre Ausrüstung anzuwenden:
- Identifizierung von Schlüsselmassen: Bestimmen Sie, welche Komponenten ein wesentliches Gewicht haben
- Federelemente ausfindig machen: Suche nach Bauteilen, die Energie speichern und wieder abgeben (echte Federn, flexible Halterungen usw.)
- Kartenverbindungen: Dokumentieren, wie Massen und Federn zusammenwirken
- Vereinfachen Sie: Kombinieren Sie ähnliche Elemente, um ein überschaubares Modell zu erstellen
Arten von Masse-Feder-Systemen
| System Typ | Beschreibung | Gemeinsame Anwendungen |
|---|---|---|
| Einzelne DOF | Eine Masse mit einer Feder | Einfache Druckluftzylinder |
| Multi-DOF | Mehrere Massen mit mehreren Federn | Komplexe Maschinen mit mehreren Komponenten |
| Kontinuierlich | Unendlich viele DOF (erfordert eine andere Analyse) | Balken, Platten und Schalen |
Erweiterte Modellierungsüberlegungen
Das grundlegende Masse-Feder-Modell ist zwar wertvoll, aber durch verschiedene Verbesserungen wird es realistischer:
- Hinzufügen von Dämpfern: Reale Systeme haben immer Energieverluste
- Berücksichtigung von Nichtlinearitäten: Die Federn folgen nicht immer Hookesches Gesetz4 perfekt
- Berücksichtigung von erzwungenen Vibrationen: Externe Kräfte verändern das Systemverhalten
- Einschließlich Kopplungseffekte: Die Bewegung in eine Richtung kann sich auf andere Richtungen auswirken
Optimierung des Dämpfungsverhältnisses: Welche Experimente führen zu den besten Ergebnissen?
Dämpfung ist der beste Schutz vor Resonanzproblemen. Die Ermittlung des optimalen Dämpfungsverhältnisses durch Experimente kann die Systemleistung und -zuverlässigkeit drastisch verbessern.
Dämpfungsverhältnis5 Bei Optimierungsexperimenten werden systematisch verschiedene Dämpfungskonfigurationen getestet, um das ideale Gleichgewicht zwischen Schwingungsdämpfung und Ansprechverhalten des Systems zu finden. Das optimale Dämpfungsverhältnis liegt in der Regel zwischen 0,2 und 0,7 und bietet eine ausreichende Schwingungsunterdrückung ohne übermäßigen Energieverlust.
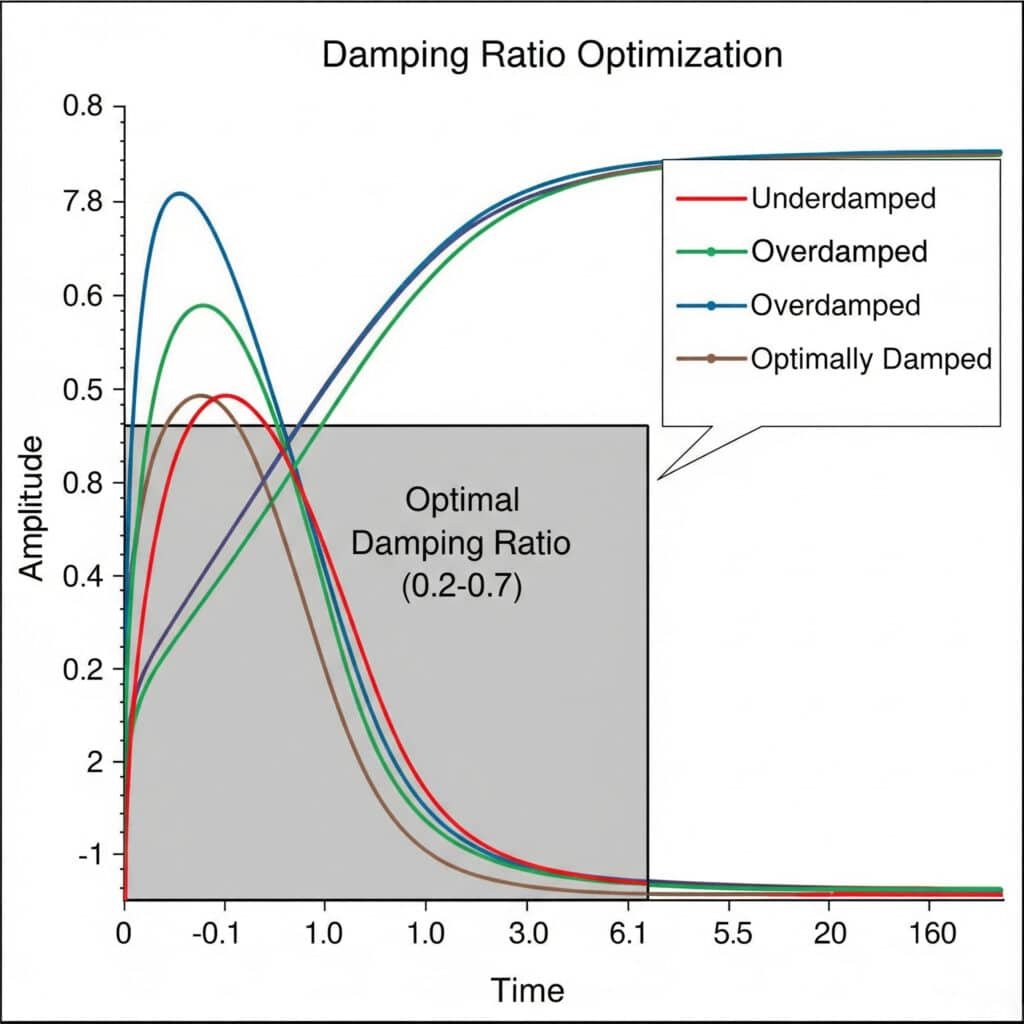
Letzten Monat habe ich einem französischen Hersteller von Lebensmittelverarbeitungsanlagen geholfen, hartnäckige Vibrationsprobleme in seinen magnetischen kolbenstangenlosen Zylindern zu lösen. Durch eine Reihe von Experimenten zum Dämpfungsverhältnis fanden wir heraus, dass die ursprüngliche Konstruktion ein Dämpfungsverhältnis von nur 0,05 aufwies - viel zu niedrig, um Resonanzprobleme zu vermeiden.
Versuchsaufbau für die Prüfung des Dämpfungsverhältnisses
Durchführung von Experimenten zur effektiven Dämpfungsoptimierung:
- Baseline-Messung: Aufzeichnung der Systemantwort ohne zusätzliche Dämpfung
- Inkrementelle Prüfung: Dämpfungselemente in kontrollierten Schritten hinzufügen
- Messung der Reaktion: Messung von Amplitude, Einschwingzeit und Frequenzgang
- Analyse der Daten: Berechnung des Dämpfungsverhältnisses für jede Konfiguration
- Validierung: Überprüfen Sie die Leistung unter realen Betriebsbedingungen
Vergleich der Dämpfungstechnologien
| Dämpfungs-Technologie | Vorteile | Beschränkungen | Typische Anwendungen |
|---|---|---|---|
| Viskose Dämpfer | Vorhersagbare Leistung, temperaturstabil | Wartung erforderlich, mögliche Lecks | Schwermaschinen, Präzisionsgeräte |
| Reibungsdämpfer | Einfaches Design, kosteneffektiv | Abnutzung im Laufe der Zeit, nichtlineares Verhalten | Strukturelle Träger, Grundmaschinen |
| Material Dämpfung | Keine beweglichen Teile, kompakt | Begrenzter Einstellbereich | Präzisionsinstrumente, Schwingungsisolierung |
| Aktive Dämpfung | Anpassungsfähig an veränderte Bedingungen | Komplex, erfordert Strom | Kritische Anwendungen, Geräte mit variabler Geschwindigkeit |
Optimierung der Dämpfung für unterschiedliche Betriebsbedingungen
Das ideale Dämpfungsverhältnis ist nicht universell - es hängt von Ihrer spezifischen Anwendung ab:
- Hochgeschwindigkeitsoperationen: Geringere Dämpfungsverhältnisse (0,1-0,3) erhalten die Reaktionsfähigkeit
- Präzisionsanwendungen: Höhere Dämpfungsverhältnisse (0,5-0,7) sorgen für Stabilität
- Systeme mit variabler Last: Adaptive Dämpfung kann erforderlich sein
- Temperaturempfindliche Umgebungen: Berücksichtigen Sie dämpfende Materialien mit stabilen Eigenschaften
Fallstudie: Optimierung der Dämpfung von kolbenstangenlosen Zylindern
Bei der Optimierung eines doppeltwirkenden kolbenstangenlosen Zylinders für eine Verpackungsmaschine haben wir fünf verschiedene Dämpfungskonfigurationen getestet:
- Standard-Endkissen: Dämpfungsverhältnis = 0,12
- Erweiterte Kissen: Dämpfungsverhältnis = 0,25
- Externe Stoßdämpfer: Dämpfungsverhältnis = 0,41
- Montagehalterungen aus Verbundwerkstoff: Dämpfungsverhältnis = 0,38
- Kombinierter Ansatz (3+4): Dämpfungsverhältnis = 0,53
Der kombinierte Ansatz lieferte die beste Leistung, indem er die Schwingungsamplitude um 78% reduzierte und gleichzeitig akzeptable Reaktionszeiten aufrechterhielt.
Schlussfolgerung
Das Verständnis von Schwingungsresonanzen durch Eigenfrequenzberechnungen, Masse-Feder-Modellierung und Optimierung des Dämpfungsverhältnisses ist entscheidend für die Vermeidung von Maschinenausfällen. Durch die Anwendung dieser Prinzipien können Sie die Lebensdauer von Maschinen verlängern, Ausfallzeiten reduzieren und die Gesamtleistung des Systems verbessern.
FAQs zur Schwingungsresonanz
Was ist Vibrationsresonanz in Industrieanlagen?
Vibrationsresonanz tritt auf, wenn eine äußere Kraft mit der Eigenfrequenz eines Systems übereinstimmt und verstärkte Schwingungen verursacht. Bei Industrieanlagen kann dieses Phänomen zu übermäßiger Bewegung, Ermüdung der Komponenten und katastrophalen Ausfällen führen, wenn es nicht richtig gehandhabt wird.
Wie kann ich feststellen, ob in meinem System Resonanz auftritt?
Achten Sie auf Symptome wie unerklärliche Geräuschzunahme, sichtbare Vibrationen bei bestimmten Drehzahlen, vorzeitige Bauteilausfälle und Leistungseinbußen, die an gleichbleibenden Betriebspunkten auftreten. Schwingungsanalysetools können Resonanzbedingungen bestätigen.
Was ist der Unterschied zwischen erzwungener Vibration und Resonanz?
Erzwungene Schwingungen treten immer dann auf, wenn eine äußere Kraft auf ein System einwirkt, während Resonanz der spezielle Zustand ist, in dem diese erzwungene Frequenz mit der Eigenfrequenz des Systems übereinstimmt, was zu einer verstärkten Reaktion führt. Jede Resonanz beinhaltet erzwungene Schwingungen, aber nicht jede erzwungene Schwingung führt zu Resonanz.
Wie wirkt sich die Konstruktion eines kolbenstangenlosen Pneumatikzylinders auf seine Schwingungseigenschaften aus?
Die Konstruktion von kolbenstangenlosen Pneumatikzylindern - mit ihrem beweglichen Schlitten, dem internen Dichtungssystem und den Führungsmechanismen - stellt besondere Anforderungen an die Vibration. Das verlängerte Profil wirkt wie ein Balken, der sich biegen kann, die Masse des Schlittens erzeugt Trägheitskräfte, und die Dichtungsbänder können variable Reibung verursachen.
Welche einfachen Änderungen können die Resonanz in bestehenden Geräten verringern?
Bei vorhandenen Geräten mit Resonanzproblemen sollten Sie überlegen, ob Sie die Eigenfrequenz durch Hinzufügen von Masse verändern, externe Dämpfer oder Stoßdämpfer einbauen, die Montagemethoden so ändern, dass sie eine Schwingungsisolierung beinhalten, oder die Betriebsgeschwindigkeit anpassen, um Resonanzfrequenzen zu vermeiden.
-
Bietet eine grundlegende Erklärung der mechanischen Resonanz, oft mit visuellen Beispielen, die zeigen, wie eine kleine periodische Kraft Schwingungen mit großer Amplitude in einem System erzeugen kann. ↩
-
Bietet einen detaillierten Einblick in die Physik der Eigenfrequenz, der spezifischen Frequenz, bei der ein System dazu neigt, in Abwesenheit jeglicher Antriebs- oder Dämpfungskraft zu schwingen. ↩
-
Erläutert die Prinzipien des Masse-Feder-Modells, einer grundlegenden Idealisierung in der Physik und im Ingenieurwesen, die zur Analyse komplexer Systeme mit einfacher harmonischer Bewegung verwendet wird. ↩
-
Einzelheiten zum Hooke'schen Gesetz, einem physikalischen Prinzip, das besagt, dass die Kraft, die erforderlich ist, um eine Feder um eine bestimmte Strecke zu verlängern oder zusammenzudrücken, direkt proportional zu dieser Strecke ist. ↩
-
Beschreibt das Dämpfungsverhältnis, ein dimensionsloses Maß, das definiert, wie Schwingungen in einem System nach einer Störung abklingen, was für die Kontrolle der Resonanz entscheidend ist. ↩


