Haben Sie ständig mit der Berechnung pneumatischer Systeme zu kämpfen? Viele Ingenieure stehen vor dem gleichen Problem, wenn sie pneumatische Systeme entwerfen oder Fehler beheben. Die gute Nachricht ist, dass die Beherrschung einiger weniger Schlüsselgleichungen die meisten Ihrer pneumatischen Herausforderungen lösen kann.
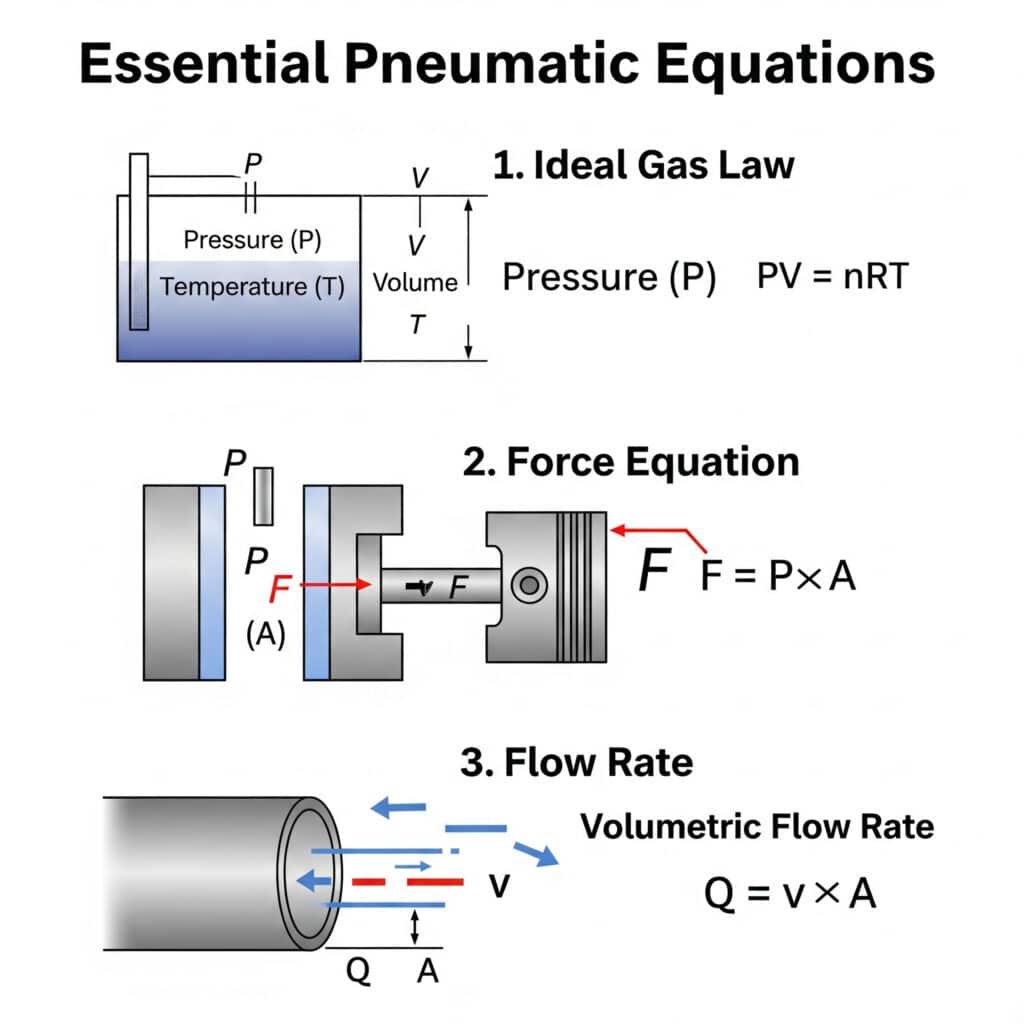
Zu den grundlegenden Gleichungen für die pneumatische Übertragung, die jeder Ingenieur kennen sollte, gehören ideales Gasgesetz (PV = nRT)1Kraftgleichung (F = P × A) und Durchflussverhältnis (Q = v × A). Die Kenntnis dieser Grundlagen ermöglicht eine genaue Systemauslegung und Fehlersuche.
Ich arbeite seit über 15 Jahren mit pneumatischen Systemen bei Bepto und habe aus erster Hand erfahren, wie das Verständnis dieser grundlegenden Gleichungen Tausende von Dollar an Ausfallzeiten einsparen und kostspielige Konstruktionsfehler verhindern kann.
Inhaltsübersicht
- Ableitung der Gasgleichung: Warum ist PV = nRT in pneumatischen Systemen von Bedeutung?
- Wie hängen Kraft, Druck und Fläche in Pneumatikzylindern zusammen?
- Wie ist das Verhältnis zwischen Durchfluss und Geschwindigkeit in pneumatischen Systemen?
- Schlussfolgerung
- FAQs über pneumatische Übertragungsgleichungen
Ableitung der Gasgleichung: Warum ist PV = nRT in pneumatischen Systemen von Bedeutung?
Bei der Entwicklung pneumatischer Systeme ist es entscheidend zu wissen, wie sich Gase unter verschiedenen Bedingungen verhalten. Dieses Wissen kann den Unterschied zwischen einem System, das zuverlässig funktioniert, und einem, das unerwartet ausfällt, ausmachen.
Das ideale Gasgesetz (PV = nRT) ist für pneumatische Systeme von grundlegender Bedeutung, da es beschreibt, wie Druck, Volumen und Temperatur zusammenwirken. Diese Beziehung hilft Ingenieuren bei der Vorhersage, wie sich die Luft in kolbenstangenlosen Zylindern und anderen pneumatischen Komponenten unter verschiedenen Betriebsbedingungen verhält.

Das Gesetz des idealen Gases mag wie ein theoretisches Konzept aus dem Physikunterricht erscheinen, aber es hat direkte praktische Anwendungen in pneumatischen Systemen. Lassen Sie mich dies in praktischere Begriffe fassen.
Verständnis der Variablen in PV = nRT
| Variabel | Bedeutung | Pneumatische Anwendung |
|---|---|---|
| P | Druck | Betriebsdruck in Ihrem System |
| V | Band | Luftkammergröße in Zylindern |
| n | Anzahl der Mole | Menge der Luft im System |
| R | Gaskonstante2 | Universelle Konstante (8.314 J/mol-K) |
| T | Temperatur | Betriebstemperatur |
Wie sich die Temperatur auf die pneumatische Leistung auswirkt
Temperaturschwankungen können die Leistung von Pneumatiksystemen erheblich beeinträchtigen. Letztes Jahr wandte sich einer unserer Kunden in Deutschland, Hans, an mich, weil die Leistung seines kolbenstangenlosen Zylindersystems uneinheitlich war. Das System funktionierte morgens einwandfrei, verlor aber am Nachmittag an Leistung.
Nach der Analyse seines Aufbaus stellten wir fest, dass das System direktem Sonnenlicht ausgesetzt war, was einen Temperaturanstieg von 15°C verursachte. Anhand des idealen Gasgesetzes berechneten wir, dass diese Temperaturänderung eine Druckschwankung von fast 5% verursachte. Wir installierten eine geeignete Isolierung, und das Problem war sofort behoben.
Praktische Anwendungen des Gasgesetzes in der pneumatischen Konstruktion
Bei der Auslegung von pneumatischen Systemen mit kolbenstangenlose Zylinderhilft uns das Gasgesetz:
- Berechnung von Druckänderungen aufgrund von Temperaturschwankungen
- Ermittlung des Volumenbedarfs für Luftbehälter
- Vorhersage von Kraftleistungsschwankungen unter verschiedenen Bedingungen
- Angemessene Dimensionierung der Kompressoren für die jeweilige Anwendung
Wie hängen Kraft, Druck und Fläche in Pneumatikzylindern zusammen?
Bei der Auswahl des richtigen kolbenstangenlosen Zylinders für Ihre Anwendung ist es wichtig, die Beziehung zwischen Kraft, Druck und Fläche zu verstehen. Dieses Wissen gewährleistet, dass Sie die benötigte Leistung erhalten, ohne zu viel Geld auszugeben.
Die Kraft-Druck-Flächen-Beziehung3 in Pneumatikzylindern ist definiert durch F = P × A, wobei F die Kraft (N), P der Druck (Pa) und A die effektive Fläche (m²) ist. Diese Gleichung ermöglicht es Ingenieuren, die genaue Kraftausgabe von kolbenstangenlosen Zylindern bei verschiedenen Betriebsdrücken zu berechnen.
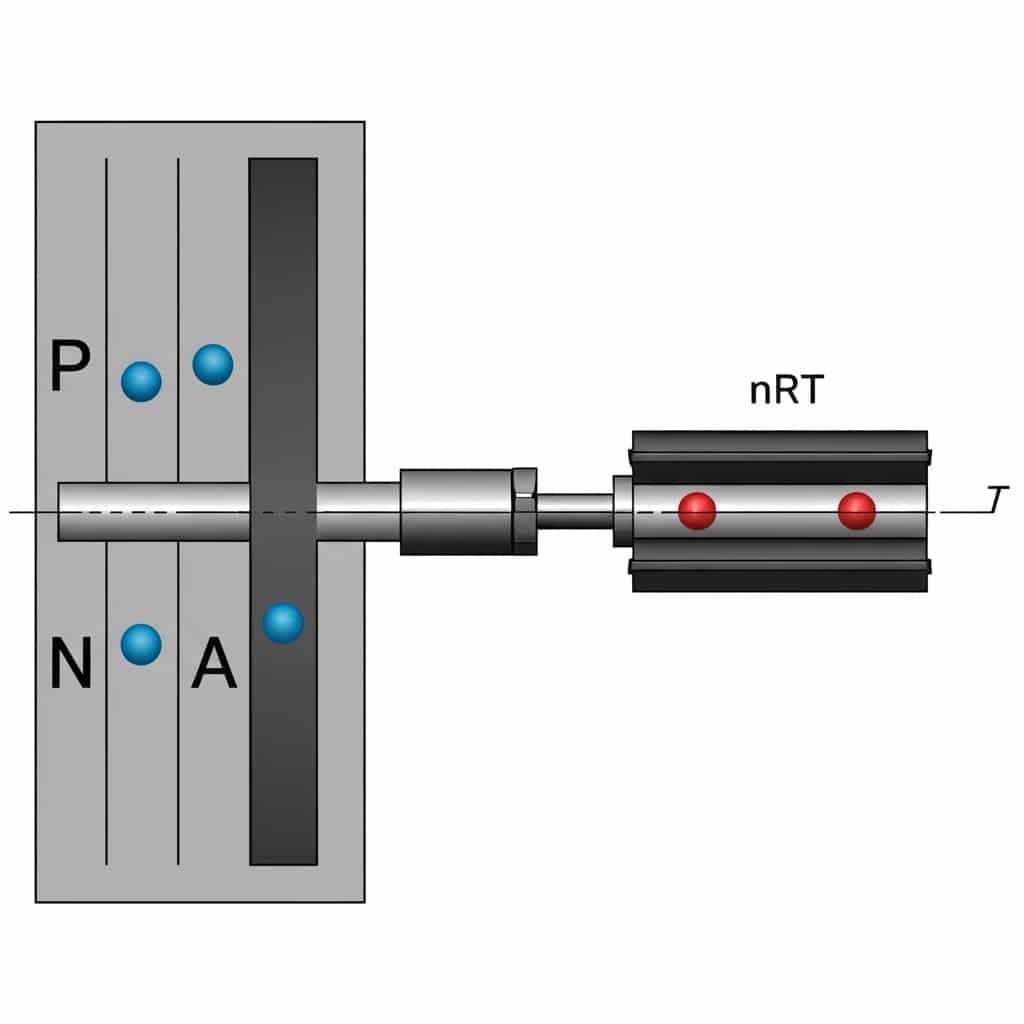
Diese einfache Gleichung ist die Grundlage aller pneumatischen Kraftberechnungen, aber es gibt einige praktische Überlegungen, die viele Ingenieure übersehen.
Berechnung der effektiven Fläche für verschiedene Zylindertypen
Die effektive Fläche variiert je nach Zylindertyp:
| Typ des Zylinders | Berechnung der effektiven Fläche | Anmerkungen |
|---|---|---|
| Einfachwirkend | A = πr² | Voller Bohrungsbereich |
| Doppeltwirkend (Verlängerung) | A = πr² | Voller Bohrungsbereich |
| Doppeltwirkend (Rückzug) | A = π(r² - r'²) | r' ist der Radius der Stange |
| Kolbenstangenloser Zylinder | A = πr² | Konsistent in beide Richtungen |
Kraft-Effizienz-Faktoren in der realen Welt
In der Praxis wird die tatsächliche Kraftleistung durch folgende Faktoren beeinflusst:
- Reibungsverluste: Typischerweise 3-20% je nach Dichtungsausführung
- Druckverluste: Kann den effektiven Druck um 5-10% reduzieren
- Dynamische Effekte: Beschleunigungskräfte können die verfügbare Kraft verringern
Ich erinnere mich an die Zusammenarbeit mit Sarah, einer Maschinenbauingenieurin aus einem Verpackungsunternehmen im Vereinigten Königreich. Sie war dabei, eine neue Maschine zu entwerfen und hatte berechnet, dass sie einen kolbenstangenlosen Zylinder mit einer Bohrung von 63 mm benötigte, um die erforderliche Kraft zu erreichen. Allerdings hatte sie die Reibungsverluste nicht berücksichtigt.
Wir empfahlen, auf einen Zylinder mit 80 mm Bohrung umzusteigen, der genug zusätzliche Kraft bot, um die Reibung zu überwinden und gleichzeitig die erforderliche Leistung beizubehalten. Diese einfache Anpassung ersparte ihr eine kostspielige Neukonstruktion nach dem Einbau.
Vergleich zwischen theoretischem und tatsächlichem Kraftaufwand
Bei der Auswahl von kolbenstangenlosen Zylindern empfehle ich immer:
- Berechnung der theoretischen Kraft mit F = P × A
- Für die meisten Anwendungen gilt ein Sicherheitsfaktor von 25%
- Überprüfung der Berechnungen anhand der tatsächlichen Leistungsdaten des Herstellers
- Gegebenenfalls Berücksichtigung dynamischer Belastungsbedingungen
Wie ist das Verhältnis zwischen Durchfluss und Geschwindigkeit in pneumatischen Systemen?
Durchflussmenge und Geschwindigkeit sind entscheidende Parameter, die bestimmen, wie schnell Ihr Pneumatiksystem reagiert. Wenn Sie diese Beziehung verstehen, können Sie eine träge Leistung verhindern und sicherstellen, dass Ihr System die Zykluszeitanforderungen erfüllt.
Die Beziehung zwischen Durchflussmenge (Q) und Geschwindigkeit (v)4 in pneumatischen Systemen ist definiert durch Q = v × A, wobei Q der volumetrische Durchfluss, v die Luftgeschwindigkeit und A die Querschnittsfläche des Durchgangs ist. Diese Gleichung ist entscheidend für die richtige Dimensionierung von Luftleitungen und Ventilen.
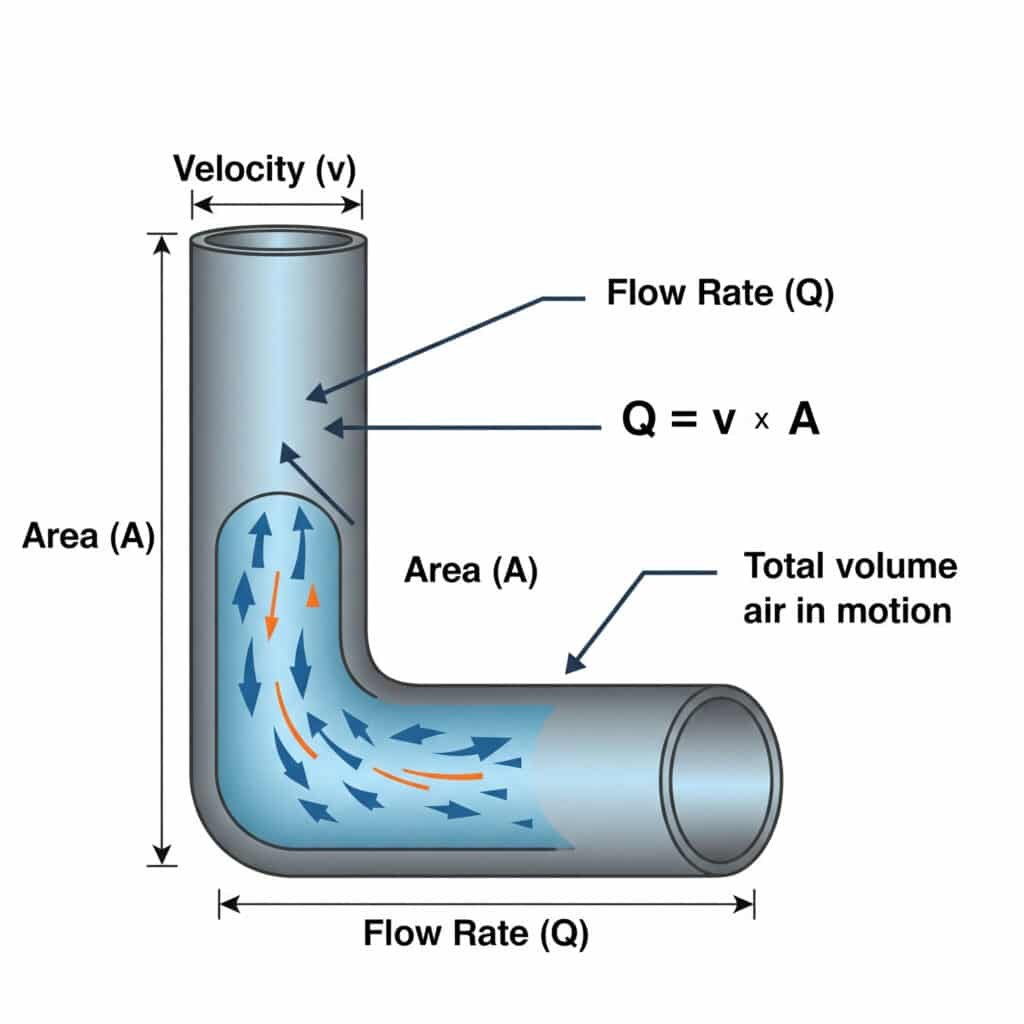
Viele Probleme mit pneumatischen Systemen sind auf eine falsche Dimensionierung der Luftversorgungskomponenten zurückzuführen. Sehen wir uns an, wie sich diese Gleichung auf die Leistung in der Praxis auswirkt.
Kritische Durchflussraten für gängige pneumatische Komponenten
Verschiedene Komponenten haben unterschiedliche Strömungsanforderungen:
| Komponente | Typische Durchflussmengenanforderung | Auswirkungen der Unterdimensionierung |
|---|---|---|
| Kolbenstangenloser Zylinder (25 mm Bohrung) | 15-30 L/min | Langsamer Betrieb, reduzierte Kraft |
| Kolbenstangenloser Zylinder (63 mm Bohrung) | 60-120 l/min | Inkonsistente Bewegung |
| Richtungssteuerungsventil | Variiert je nach Größe | Druckabfall, langsame Reaktion |
| Luftaufbereitungsanlage | System insgesamt + 30% | Druckschwankungen |
Wie sich der Rohrdurchmesser auf die Systemleistung auswirkt
Der Durchmesser Ihrer Luftleitungen hat einen dramatischen Einfluss auf die Systemleistung:
- Druckverlust: Steigt mit dem Quadrat der Geschwindigkeit
- Reaktionszeit: Kleinere Linien bedeuten höhere Geschwindigkeit, aber mehr Widerstand
- Energie-Effizienz: Größere Leitungen verringern den Druckabfall, erhöhen aber die Kosten
Berechnung der korrekten Leitungsgrößen für pneumatische Systeme
Zur richtigen Dimensionierung der Luftleitungen für Ihre kolbenstangenlose Zylinderanwendung:
- Bestimmen Sie die erforderliche Durchflussmenge anhand von Zylindergröße und Zykluszeit
- Berechnen Sie den maximal zulässigen Druckabfall (normalerweise 0,1 bar oder weniger)
- Wählen Sie einen Leitungsdurchmesser, der die Geschwindigkeit unter 15-20 m/s hält.
- Prüfen Sie die Durchflusskapazität des Ventils (Cv- oder Kv-Wert5) entspricht den Systemanforderungen
Ich habe einmal einem Kunden in Frankreich geholfen, der trotz eines großen Kompressors eine langsame Zylinderbewegung erlebte. Das Problem lag nicht in einer unzureichenden Lufterzeugung, sondern darin, dass seine 6-mm-Schläuche einen zu großen Widerstand erzeugten. Die Aufrüstung auf 10-mm-Leitungen löste das Problem sofort und erhöhte die Zyklusrate seiner Maschine um 40%.
Schlussfolgerung
Das Verständnis dieser drei grundlegenden pneumatischen Gleichungen - das ideale Gasgesetz, die Beziehung zwischen Kraft, Druck und Fläche sowie die Verbindung zwischen Durchflussrate und Geschwindigkeit - bildet die Grundlage für eine erfolgreiche pneumatische Systemauslegung. Durch die Anwendung dieser Prinzipien können Sie die richtigen kolbenstangenlosen Zylinderkomponenten auswählen, Probleme effektiv beheben und die Systemleistung optimieren.
FAQs über pneumatische Übertragungsgleichungen
Was ist das ideale Gasgesetz und warum ist es für pneumatische Systeme wichtig?
Das ideale Gasgesetz (PV = nRT) beschreibt, wie Druck, Volumen, Temperatur und Gasmenge in einem pneumatischen System zusammenhängen. Es ist wichtig, weil es Ingenieuren hilft, vorherzusagen, wie sich veränderte Bedingungen (insbesondere die Temperatur) auf die Systemleistung und die Druckanforderungen auswirken werden.
Wie berechne ich die Kraftausgabe eines kolbenstangenlosen Zylinders?
Berechnen Sie die ausgegebene Kraft durch Multiplikation des Drucks mit der effektiven Fläche (F = P × A). Bei einem kolbenstangenlosen Zylinder ist die wirksame Fläche in beiden Richtungen gleich, was die Kraftberechnung einfacher macht als bei herkömmlichen Zylindern, die unterschiedliche Ausfahr- und Einzugskräfte haben.
Was ist der Unterschied zwischen Durchflussmenge und Geschwindigkeit in pneumatischen Systemen?
Die Durchflussmenge ist das Luftvolumen, das sich pro Zeiteinheit durch ein System bewegt (normalerweise in L/min), während die Geschwindigkeit die Geschwindigkeit ist, mit der sich die Luft durch einen Durchgang bewegt (in m/s). Sie sind durch die Gleichung Q = v × A miteinander verbunden, wobei A die Querschnittsfläche des Kanals ist.
Wie wirkt sich die Temperatur auf die Leistung eines pneumatischen Systems aus?
Nach dem idealen Gasgesetz wirkt sich die Temperatur direkt auf den Druck aus. Ein Temperaturanstieg von 10°C kann den Druck um etwa 3,5% erhöhen, wenn das Volumen konstant bleibt. Dies kann zu Druckschwankungen führen, die Dichtungsleistung beeinträchtigen und die Kraftabgabe in kolbenstangenlosen Zylindern verändern.
Was ist die häufigste Ursache für Druckabfall in pneumatischen Systemen?
Die häufigsten Ursachen für Druckabfall sind unterdimensionierte Luftleitungen, restriktive Armaturen und eine unzureichende Durchflusskapazität des Ventils. Gemäß der Durchflussgleichung erfordern kleinere Durchgänge eine höhere Luftgeschwindigkeit, was den Widerstand und den Druckabfall exponentiell erhöht.
Wie dimensioniere ich Luftleitungen für einen kolbenstangenlosen Zylinder richtig?
Wählen Sie dann einen Leitungsdurchmesser aus, der die Luftgeschwindigkeit unter 15-20 m/s hält, um den Druckabfall zu minimieren. Für die meisten kolbenstangenlosen Zylinderanwendungen bieten 8-12 mm Leitungen ein gutes Gleichgewicht zwischen Leistung und Kosten.
-
Bietet eine detaillierte Erläuterung des idealen Gasgesetzes, der grundlegenden Zustandsgleichung für ein hypothetisches ideales Gas, die das Verhalten vieler Gase unter verschiedenen Bedingungen annähernd beschreibt. ↩
-
Erklärt die Rolle und den Wert der universellen Gaskonstante (R) im idealen Gasgesetz, die als physikalische Konstante dient und die Energieskala mit der Temperaturskala verbindet. ↩
-
Bietet eine grundlegende Erklärung des Drucks, definiert als die Kraft, die senkrecht auf die Oberfläche eines Objekts pro Flächeneinheit ausgeübt wird, über die diese Kraft verteilt wird. ↩
-
Erläutert das Prinzip der Kontinuitätsgleichung, eines grundlegenden Konzepts der Strömungslehre, das besagt, dass der Massendurchfluss eines inkompressiblen Fluids von einem Querschnitt eines Rohrs zum anderen konstant sein muss. ↩
-
Bietet eine technische Definition des Durchflusskoeffizienten (Cv) und des Durchflussfaktors (Kv), bei denen es sich um standardisierte Werte handelt, die zum Vergleich der Durchflusskapazitäten verschiedener Ventile verwendet werden. ↩



